Условия максимума и минимума интерференции

Явление наложения когерентных световых волн, в результате которого наблюдается чередование усиления света в одних точках пространства и ослабления в других, называют интерференцией света.

Необходимым условием интерференции света является когерентность складываемых синусоидальных волн.

Волны называют когерентными, если не изменяется с течением времени разность фаз складываемых волн, т. е. Dj = const.

Этому условию удовлетворяют монохроматические волны, т.е. волны равных частот (w₁ = w₂ = w). В силу поперечности электромагнитных (световых) волн условие когерентности является недостаточным для получения устойчивой интерференционной картины.

Достаточное условие заключается в том, чтобы колебания векторов 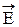, складываемых электромагнитных полей совершались вдоль одного и того же или близких направлений. При этом должно происходить совпадение не только векторов 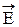, но и 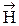, что будет наблюдаться лишь в том случае, если волны распространяются вдоль одной и той же прямой, т.е. являются одинаково поляризованными.

Найдем условия максимума и минимума интерференции.

Для этого рассмотрим сложение двух монохроматических, когерентных световых волн одинаковой частоты (w₁ = w₂ = w), имеющих равные амплитуды (Е₀₁ = Е₀₂ = Е₀), совершающих колебания в вакууме в одном направлении по закону синуса (или косинуса) , т. е.

Е₁ = Е₀₁sin(wt - kr₁ + j₀₁), (7.14)

Е₂ = Е₀₂sin(wt - kr₂ + j₀₂), (7.15)

где r₁, r₂ - расстояния от источников S₁ и S₂ до точки наблюдения на экране;

j₀₁, j₀₂ - начальные фазы; k = 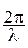- волновое число.

Согласно принципу суперпозиции (установлен Леонардо да Винчи) вектор напряженности результирующего колебания равен геометрической сумме векторов напряженности складываемых волн,

т. е.

.

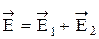Для простоты положим, что начальные фазы складываемых волн равны нулю, т. е. j₀₁ = j₀₂ = 0. По абсолютной величине, имеем

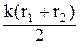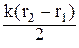Е = Е₁ + Е₂ =2Е₀sin[wt- ]×cos . (7.16)

В (7.16) выражение (r₂ - r₁)×n = d - оптическая разность хода складываемых волн; n - абсолютный показатель преломления среды.

Для других сред отличных от вакуума, например, для воды (n₁, l₁), стекла (n₂, l₂) и т. д. k = k₁ n₁; k = k₂ n₂; l=l₁n₁; l=l₂ n₂ ;

k₁= 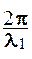; k₂= ,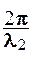

где l - длина волны света в вакууме,

Из формулы (7.16) следует, что результирующая электромагнитная волна изменяется со временем с той же циклической частотой w.

Множитель cos 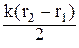не зависит от времени, поэтому величину

Е_0,рез = 2Е₀cos 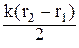(7.17)

- называют амплитудой результирующей волны.

Амплитуда мощности волны определяется (для единицы поверхности фронта волны) вектором Пойнтинга, т. е. по модулю

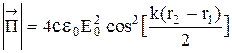, (7.18)

где½ 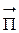½= с×w, w = e₀E² - средняя, объемная плотность энергии электромагнитного поля (для вакуума e =1), т. е. ½ 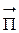½= с ×e₀E².

Если J=½ 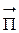½- интенсивность результирующей волны, а

J₀ = с×e₀ -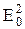

максимальная интенсивность ее, то с учетом (7.17) и (7.18) интенсивность результирующей волны будет изменяться по закону

J = 2J₀{1+ сos[k(r₂ - r₁)]}. (7.19)

Разность фаз складываемых волн

Dj = j₂ - j₁ = 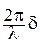=сonst (7.20)

и не зависит от времени, где

j₂ = wt - kr₂ + j₀₂; j₁ = wt - kr₁ + j₀₁.

Амплитуду результирующей волны найдем по формуле

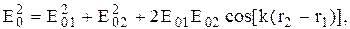(7.21)

где Dj = k(r₂ - r₁)n = 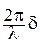. (7.22)

Возможны два случая:

Условие максимума.

Если разность фаз складываемых волн равна четному числу p

Dj = 2mp,

где m = 0, ±1, ±2, ... , то результирующая амплитуда будет максимальной,

т. е.

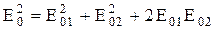(7.23)

или Е₀ = Е₀₁ + Е₀₂. (7.24)

Следовательно, амплитуды волн складываются, а при их равенстве

(Е₀₁ = Е₀₂) результирующая амплитуда - удваивается.

Результирующая интенсивность также максимальна:

J_max = 4J₀. (7.25)

Используя формулу (7.22), находим условие максимума для оптической разности хода d, т. е.

Dj^мах = 2mp = 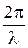d, (7.26)

d^мах = 2m 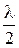. (7.27)

Вывод: Оптическая разность хода равна четному числу полуволн.

Условие минимума.

Если разность фаз складываемых волн равна нечетному числу p

Dj = (2m + 1) p,

где m = 0, ±1, ±2, ... , то амплитуда будет минимальной,

т.е.

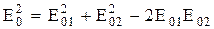(7.28)

или

Е₀ = ½Е₀₁ - Е₀₂½. (7.29)

Следовательно, амплитуды волн вычитаются, а при Е₀₁ = Е₀₂ результирующая амплитуда равна нулю.Результирующая интенсивность минимальна при: J_min = 0. (7.30)

Используя формулу (7.23), получаем условие минимума для оптической разности хода d, т. е.

Dj^min = (2m + 1)p = 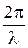d, (7.31)

d^min = (2m + 1) 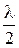. (7.32)

Вывод: Оптическая разность хода равна нечетному числу полуволн.

Таким образом, только когерентные световые волны дают устойчивую во времени интерференционную картину.

При этом результирующая интенсивность изменяется по закону

J = J₁ +J₂ +2 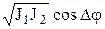, (7.33)

так как J ~ E².

Однако все естественные источники света некогерентны.

Приемники их излучения (глаз, термоэлементы, болометры и др.) воспринимают только среднюю освещенность. В этом случае среднее по времени значение cos[k(r₂ - r₁)] = 0, поэтому происходит простое сложение интенсивностей света, т. е. J = J₁ + J₂.

Следовательно, некогерентные источники при сложении их излучения не дают интерференционной картины.

Вывод: В результате интерференции света на экране наблюдается чередование максимумов и минимумов. При этом происходит перераспределение энергии световых волн между соседними областями пространства и выполняется закон сохранения энергии.