Нечетко-множественное моделирование
Качества продукции
Неточность и неполнота исходной информации приводят к необходимости применения специальных методов оценки качества товаров. Перспективным направлением для решения этой задачи является использование методов нечеткого моделирования, положительно зарекомендовавших себя в ряде социально-экономических исследований.
Важное достоинство методов нечеткого моделирования состоит в том, что они не требуют больших затрат времени и средств по сравнению с традиционными методами на получение точных исходных данных, что, может быть, в принципе, невозможно.
Появление целого ряда коммерческих программных средств, ориентированных на решение задач нечеткого моделирования, свидетельствует об эффективности применения методов нечеткого моделирования для решения практических задач.
В основе методов нечеткого моделирования лежит понятие нечеткого множества.
Нечетное множество (fuzzyset) представляет собой совокупность элементов произвольной природы, относительно которых нельзя с полной определенностью утверждать – принадлежит ли тот или иной элемент рассматриваемой совокупности данному множеству или нет.
Формально нечетное множество определяется как множество упорядоченных пар или кортежей вида:
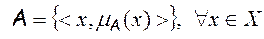 , (5.7)
, (5.7)
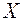 – универсальное множество (универсум), содержащее в рамках нечеткого множества элемент
– универсальное множество (универсум), содержащее в рамках нечеткого множества элемент 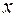 ;
;
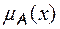 – функция принадлежности элемента
– функция принадлежности элемента 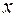 нечеткому множеству
нечеткому множеству 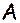 ,
, 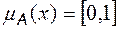 .
.
Множество 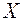 представляет собой так называемый носитель нечеткого множества, то есть обычное (четкое) множество элементов
представляет собой так называемый носитель нечеткого множества, то есть обычное (четкое) множество элементов 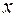 .
.
Функция принадлежности (membership function) – математическая функция, определяющая степень или уверенность, с которой элемент множества 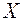 принадлежит заданному нечетному множеству
принадлежит заданному нечетному множеству 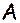 . Данная функция ставит в соответствие каждому элементу
. Данная функция ставит в соответствие каждому элементу 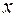 действительное число из интервала [0,1]. Чем ближе это число к единице, тем больше степень или уверенность, с которой элемент
действительное число из интервала [0,1]. Чем ближе это число к единице, тем больше степень или уверенность, с которой элемент 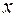 принадлежит нечетному множеству
принадлежит нечетному множеству 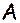 .
.
Выбор функции принадлежности является творческой задачей эксперта или группы экспертов. В принципе, вид функции принадлежности может быть выбран любым. Однако для упрощения расчетов и сокращения объема исходной информации целесообразно использовать те из них, которые допускают аналитическое представление в виде простой математической функции. Выбор типовых функций принадлежности должен быть согласован с возможностями их программной реализации в используемых инструментальных средствах.
Заданные на множестве действительных чисел нечеткие множества называются нечеткими величинами. С точки зрения аналитической обработки, наиболее удобны простейшие частные случаи нечетких величин с кусочно-линейными функциями принадлежности. В зависимости от вида функции принадлежности, различают такие нечеткие величины, как треугольное нечетное число (рис. 5.2. а), трапециевидный нечетный интервал (рис. 5.2. б), нечеткие величины с Z-образной и S-образной кусочно-линейными функциями принадлежности (рис. 5.2 в и 5.2. г соответственно).
 |
Рис. 5.2. Примеры оценок показателей качества товара
в виде нечетких величин
Треугольное нечеткое число может быть представлено в виде кортежа из трех чисел:
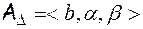 , (5.8)
, (5.8)
где 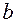 – модальное значение треугольного числа, которому соответствует функция принадлежности
– модальное значение треугольного числа, которому соответствует функция принадлежности 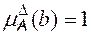 ;
; 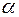 и
и 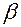 – левый и правый коэффициенты нечеткости треугольного нечеткого числа
– левый и правый коэффициенты нечеткости треугольного нечеткого числа 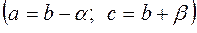 .
.
Для оценки качества продукции, помимо понятия нечеткого числа, требуется использоваться понятие лингвистической переменной.
Лингвистическая переменная характеризуется наименованием и множеством значений (термов), каждое из которых определяется своей функцией принадлежности. Примером лингвистической переменной является «Уровень качества товара», а значениями этой лингвистической переменной могут быть: «Средний уровень качества» с функцией принадлежности 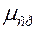 , «Высокий уровень качества» с функцией принадлежности
, «Высокий уровень качества» с функцией принадлежности 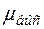 и т. д.
и т. д.
Метод нечеткой оценки качества товара включает в себя три этапа:
I. Фаззификация системы первичных показателей оценки качества.
II. Вывод итогового показателя оценки качества в виде нечеткого числа.
III. Дефаззификация показателя оценки качества.
Рассмотрим содержание этих этапов.
I. Под фаззификацией (fuzzification) в рассматриваемом методе понимается процесс получения значений функций принадлежности для термов лингвистических переменных, представляющих первичные показатели системы оценки качества.
Принимая за основу для измерения значений показателя уровня качества 100-балльную шкалу отношений, можно рекомендовать следующие лингвистические значения показателей уровня качества товара:
1. Очень низкий уровень качества. Этот уровень ниже минимально необходимого в соответствии с сертификационными требованиями к данному показателю качества товара.
2. Низкий (начальный) уровень качества, соответствующий минимальным сертификационным требованиям.
3. Средний уровень качества, характерный для предприятий, продолжительно и успешно осуществляющих производство товаров данного наименования.
4. Высокий уровень качества, характерный для элитных товаров, достигших мирового уровня качества.
5. Очень высокий уровень качества, выходящий за пределы 100-балльной шкалы и отражающий тот факт, что нет предела в совершенствовании качества товара.
На рисунке 5.3 изображены графики функций принадлежности термов лингвистической переменной «Значения показателя уровня качества товара» и интервалы оценки.
Точки пересечения соответствующих функций принадлежности: 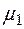 ,
, 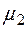 ,
, 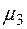 ,
, 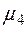 ,
, 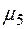 – определяют интервалы оценки качества по интервальной шкале отношений.
– определяют интервалы оценки качества по интервальной шкале отношений.
Значения показателей оценки уровня качества по шкале отклонений приведены в таблице 5.1.
 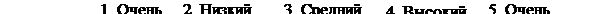 |
Рис. 5.3. Графики функций принадлежности термов
лингвистической переменной «Значения показателя уровня качества
товара» и интервалы оценки
Таблица 5.1.
Значения показателей оценки уровня качества товара
по шкале отношений
| Уровень качества, термы | 1. Очень низкий уровень качества | 2. Низкий (начальный) уровень качества | 3. Средний уровень качества | 4. Высокий уровень качества | 5. Очень высокий уровень качества | |||||
| Интервальная оценка качества, баллы | 0 – 20 | 20 – 44 | 45 – 75 | 76 – 100 | 100 – 120 | |||||
| Длина интервала, баллы | - | |||||||||
| Модальное значение функции принадлежности, баллы | 0 – 10 | 110 – 120 | ||||||||
| Левый и правый коэффициенты нечеткости треугольного нечеткого числа, баллы | ||||||||||
Сущность фаззификации состоит в следующем.
Процесс получения оценки первичного показателя качества начинается с того, что эксперт дает четкую оценку качества по шкале отношений (точечную или интервальную). Далее эта четкая оценка заменяется нечеткой оценкой в виде соответствующего значения (терма) лингвистической переменной.
Помимо показателей уровня качества, входными величинами в соответствии с предлагаемой моделью оценки качества являются весовые коэффициенты показателей. В качестве весовых коэффициентов показателей предлагается использовать пять вариантов треугольных нечетких чисел (рисунок 5.4). Эти нечеткие числа подобраны таким образом, чтобы можно было составить разнообразные их комбинации так, чтобы сумма модальных значений коэффициентов в каждой комбинации равнялась единице.
В таблице 5.2 приведены значения весовых коэффициентов как термов лингвистической переменной и их параметров как треугольных чисел.
  |
Рис. 5.4. Графики функций принадлежности термов
лингвистической переменной «Весовой коэффициент показателя»:
1 – очень малый, 2 – малый, 3 – средний, 4 – большой, 5 – очень большой
Таблица 5.2.
Значения весовых коэффициентов
| Значения лингвистической переменной «Весовой коэффициент показателя», термы | 1. Очень малый | 2. Малый | 3. Средний | 4. Большой | 5. Очень большой | |||||
| Модальное значение функции принадлежности, доли единицы | 0,05 | 0,1 | 0,2 | 0,5 | 0,6 | |||||
| Левый и правый коэффициенты нечеткости треугольного нечеткого числа, доли единицы | 0,1 | 0,05 | 0,2 | 0,1 | 0,3 | 0,4 | 0,6 | 0,5 | 0,7 | |
II. Вывод итогового показателя оценки качества.
Принципиальный алгоритм нечеткой оценки качества расчета сводится к получению парных произведений частных показателей качества в виде треугольных нечетких чисел и соответствующих весовых коэффициентов, представленных также в виде треугольных нечетких чисел, с последующим сложением этих парных произведений.
Алгоритм нечеткого вывода оценки качества товара может быть представлен следующим образом:
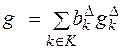 , (5.9)
, (5.9)
где 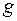 – значение интегрального показателя качества;
– значение интегрального показателя качества; 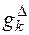 – значение k-го частного показателя качества в виде треугольного нечеткого числа;
– значение k-го частного показателя качества в виде треугольного нечеткого числа; 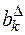 – весомый коэффициент k-го частного показателя качества в виде треугольного нечеткого числа;
– весомый коэффициент k-го частного показателя качества в виде треугольного нечеткого числа; 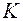 – множество частных показателей качества товара.
– множество частных показателей качества товара.
Таким образом, в предлагаемом алгоритме вывода итогового показателя оценки качества присутствуют операции умножения треугольных нечетких чисел. В результате выполнения этих операций также получается треугольное нечеткое число, рассчитываемое в соответствии со следующими формулами.
Пусть 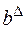 и
и 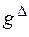 ‑ два треугольных нечетких числа (показатель качества и его весовой коэффициент), заданных параметрически в виде кортежей:
‑ два треугольных нечетких числа (показатель качества и его весовой коэффициент), заданных параметрически в виде кортежей:
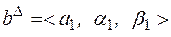 (5.10)
(5.10)
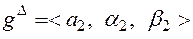 . (5.11)
. (5.11)
Тогда парное произведение этих чисел равняется
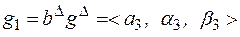 , (5.12)
, (5.12)
где параметры 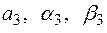 определяются следующим образом:
определяются следующим образом:
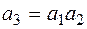 , (5.13)
, (5.13)
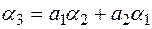 , (5.14)
, (5.14)
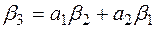 , (5.15)
, (5.15)
В некоторых программных продуктах, например в системе MATLAB, нечеткие коэффициенты вычисляются в соответствии с формулами:
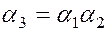 , (5.16)
, (5.16)
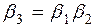 . (5.17)
. (5.17)
Сложение двух треугольных нечетких чисел (результатов парных произведений в предлагаемом алгоритме)
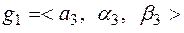 (5.18)
(5.18)
и
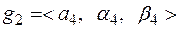 (5.19)
(5.19)
приводит к появлению следующего треугольного числа:
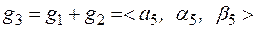 , (5.20)
, (5.20)
где параметры 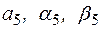 определяются следующим образом:
определяются следующим образом:
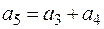 , (5.21)
, (5.21)
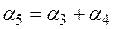 , (5.22)
, (5.22)
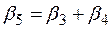 . (5.23)
. (5.23)
III. Дефаззификация итогового показателя оценки качества.
Итоговый показатель оценки качества, получаемый в результате свертки частных нечетких показателей в виде треугольных нечетких чисел, представляет собой нечетное треугольное число.
В соответствии с предлагаемым методом для практического использования итогового показателя предусматривается его дефаззификация. Дефаззификация (defuzzification) означает получение четкой интервальной оценки или единственного количественного значения показателя.
Для целей дефаззификации предлагается использовать понятие четкого множества (интервала), ближайшего к нечетному множеству (интервалу).
Характеристическая функция ближайшего четкого множества А, по отношению к нечеткому множеству A определяется следующим выражением:
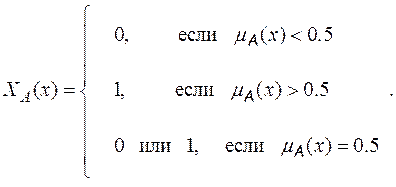 (5.24)
(5.24)
Характеристическая функция принимает значение 1 для каждого элемента данного четкого множества и значение 0 для всех остальных элементов, не входящих в данное множество.
Рисунок 5.5. иллюстрирует переход от нечеткого множества к ближайшему четкому множеству.
 |
Рис. 5.5. Переход от нечеткого множества
к ближайшему четкому множеству
Для приведения значения показателя уровня качества к единственному числу интервальная оценка может быть заменена средним значением четного интервала (медианой).
Нечеткое моделирование оценки качества продукции может осуществляться в среде MATLAB и fuzzy TECH.
Дата добавления: 2016-02-04; просмотров: 1005;
