Притоков денежных средств
Случайный характер притоков денежных средств связан с двумя группами факторов.
В случае производства продукции «на склад» случайная величина объёма реализации в каждом подпериоде зависит от тренда, сезонных и случайных колебаний спроса и цены продукции.
Рис. 2.8. Платежное поручение исходящее
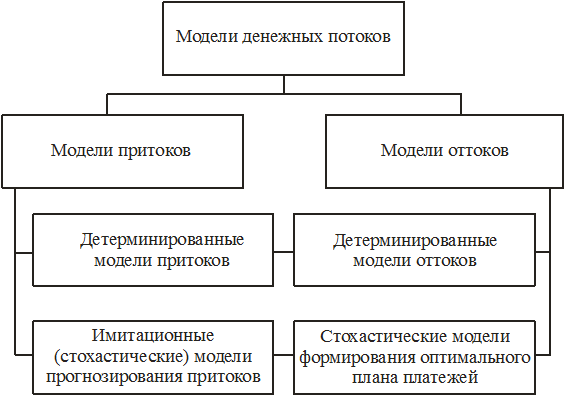
Рис. 2.9. Взаимосвязь моделей денежных потоков
В случае производства продукции «на заказ» (по договору) случайной величиной является подпериод поступления денежных средств, вероятность распределения которой зависит от значения признаков классификации покупателей продукции.
К этим признакам относятся: продолжительность деловых контактов, финансовое состояние покупателя, его принадлежность к числу отечественных или зарубежных и др.
На рисунке 2.10 представлены графики зависимости вероятности притока денежных средств от даты для различных категорий клиентов корпорации.

Рис. 2.10. Вероятность поступления денежных средств по дням месяца
для различных категорий покупателей
В зависимости от класса клиента можно с разной вероятностью ожидать поступления денежных средств на расчетные счета корпорации:
1. иностранные покупатели;
2. временные покупатели;
3. покупатели, срок сотрудничества с которыми составляет от 5 до 10 лет, и финансовое положение которых устойчивое;
4. покупатели, срок сотрудничества с которыми составляет от 5 – до 10 лет, и финансовое положение которых неустойчивое.
5. покупатели, срок сотрудничества с которыми составляет от 10 лет, и финансовое положение которых устойчивое.
6. покупатели, срок сотрудничества с которыми составляет от 10 лет, и финансовое положение которых неустойчивое.
На основании такой статистики строится имитационная модель поступления денежных средств (рисунок 2.11). Основой имитационного моделирования является генерация случайных сроков поступления денежных средств в соответствии с принятыми законами распределения для классов клиентов.
Затем проводятся многократные имитационные эксперименты, в каждом из которых подсчитываются величина притоков по каждому дню месяца и сальдо притоков. После завершения имитационных экспериментов осуществляет обработка статистических данных, полученных в каждом эксперименте.
Чем больше число экспериментов в имитационном моделировании, тем меньше разница между получаемыми статистическими оценками числовых характеристик случайных величин, поскольку в большей степени статистические оценки сходятся по вероятности к соответствующим числовым характеристикам.
Пользуясь методом имитационного (статистического моделирования), мы приближенно заменяем математические ожидания случайных величин их средними арифметическими значениями (статистическими оценками).
Определение числа экспериментов, необходимого для обеспечения заданной точности, основывается на центральной предельной теореме теории вероятностей. Согласно этой теореме, при большом числе имитационных экспериментов среднее арифметическое значение 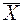 случайной величины X является нормально распределенной случайной величиной.
случайной величины X является нормально распределенной случайной величиной.

Рис. 2.11. Блок-схема имитационного моделирования
В этом случае вероятность отклонения величины 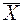 от ее математического ожидания вычисляется по формуле:
от ее математического ожидания вычисляется по формуле:
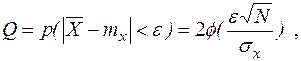 (2.9)
(2.9)
где 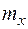 ‑ математическое ожидание величины X;
‑ математическое ожидание величины X; 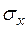 ‑ среднеквадратическое отклонение;
‑ среднеквадратическое отклонение; 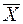 ‑ среднее арифметическое наблюдаемых значений величины X, получаемых в результате имитационных экспериментов; N ‑ количество имитационных экспериментов;
‑ среднее арифметическое наблюдаемых значений величины X, получаемых в результате имитационных экспериментов; N ‑ количество имитационных экспериментов; 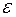 ‑ верхняя граница ошибки;
‑ верхняя граница ошибки; 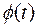 ‑ функция Лапласа (
‑ функция Лапласа ( 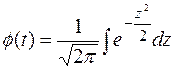 ).
).
Обычно в практике имитационного моделирования неизвестно среднее квадратическое отклонение интересующей нас случайной величины Х. В этом случае для приближенной оценки точности моделирования вместо 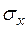 можно воспользоваться статистической оценкой этой величины, полученной в серии из N имитационных экспериментов:
можно воспользоваться статистической оценкой этой величины, полученной в серии из N имитационных экспериментов:
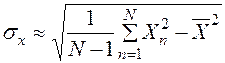 . (2.10)
. (2.10)
Верхняя граница ошибки уменьшается с увеличением числа имитационных экспериментов в соответствии с формулой:
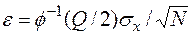 , (2.11)
, (2.11)
где 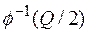 ‑ функция, обратная функции Лапласа, то есть такое значение аргумента этой функции, при котором функция Лапласа
‑ функция, обратная функции Лапласа, то есть такое значение аргумента этой функции, при котором функция Лапласа 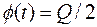 .
.
Число имитационных экспериментов, необходимое для того, чтобы с заданной вероятностью (уровнем доверия) 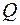 среднее арифметическое
среднее арифметическое 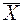 полученных значений случайной величины не отличалось от ее математического ожидания более чем на
полученных значений случайной величины не отличалось от ее математического ожидания более чем на 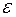 , равняется:
, равняется:
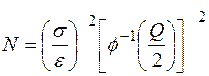 . (2.12)
. (2.12)
Результатом имитационного (стохастического) моделирования являются числовые характеристики сальдо притоков:
· статистическая оценка сальдо притоков, приходящегося на  -й подпериод:
-й подпериод:
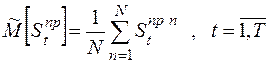 ; (2.13)
; (2.13)
· статистическая оценка среднего квадратического отклонения сальдо притоков, приходящегося на  -й подпериод:
-й подпериод:
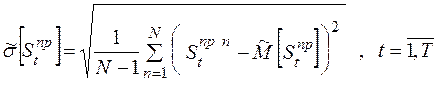 ; (2.14)
; (2.14)
· статистический коэффициент вариации сальдо притоков, приходящегося на  -й подпериод:
-й подпериод:
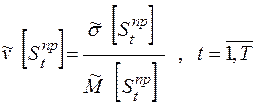 ; (2.15)
; (2.15)
· максимальное значение сальдо притоков, приходящегося на  -й подпериод:
-й подпериод:
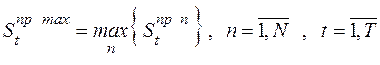 ; (2.16)
; (2.16)
· минимальное значение сальдо притоков, приходящегося на  -й подпериод:
-й подпериод:
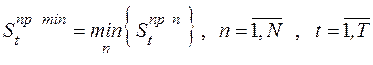 . (2.17)
. (2.17)
Пороговое значение сальдо притоков, которое будет достигнуто или превышено с заданной вероятностью определяется в соответствии с формулой:
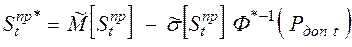 , (2.18)
, (2.18)
где 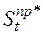 – значение сальдо притоков денежных средств, которое будет достигнуто или превышено с вероятностью
– значение сальдо притоков денежных средств, которое будет достигнуто или превышено с вероятностью 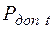 ;
; 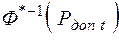 – функция, обратная по отношению к нормальной функции распределения
– функция, обратная по отношению к нормальной функции распределения 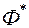 .
.
Дата добавления: 2016-02-04; просмотров: 865;
