Оптимизационная модель и инструментальные средства
формирования плана платежей
Предлагаемая модель формирования оптимального плана платежей может быть использована как в оперативном, так и в тактическом финансовом планировании.
Отличительной особенностью модели является использование пошагового принципа анализа остатка денежных активов с учётом временной ценности денег в сочетании с требованиями постановки задачи линейного программирования с булевыми переменными.
Модель позволяет распределить заданное множество платежей по подпериодам планового периода в соответствии с поступлениями денежных средств таким образом, чтобы избежать овердрафта и при этом минимизировать потери, связанные с оттоком денег, штрафными санкциями, краткосрочным кредитованием и т.д.
Математическая постановка задачи имеет следующий вид:
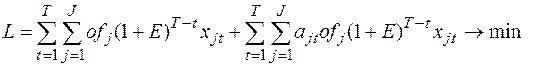 (2.19)
(2.19)
 (2.20)
(2.20)
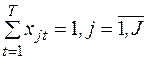 (2.21)
(2.21)
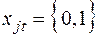 (2.22)
(2.22)
Здесь приняты следующие обозначения: 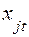 – двоичная переменная, принимающая значение «1», если
– двоичная переменная, принимающая значение «1», если 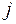 -й платёж предусматривается по плану произвести в
-й платёж предусматривается по плану произвести в  -й подпериод, и «0» – в противном случае;
-й подпериод, и «0» – в противном случае; 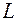 – суммарная величина потерь по всем платежам;
– суммарная величина потерь по всем платежам;  – сумма
– сумма 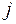 -го платежа;
-го платежа;  – множество платежей;
– множество платежей; 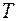 – количество подпериодов;
– количество подпериодов; 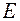 – ставка размещения, характеризующая реальные возможности по использования части временно свободных денежных средств;
– ставка размещения, характеризующая реальные возможности по использования части временно свободных денежных средств; 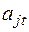 – относительная оценка потерь, связанных с задержкой платежа до
– относительная оценка потерь, связанных с задержкой платежа до  -го подпериода (ставка штрафа, ставка по краткосрочному кредиту, экспертная оценка потерь);
-го подпериода (ставка штрафа, ставка по краткосрочному кредиту, экспертная оценка потерь); 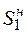 – сальдо накопленных денежных средств на начало первого подпериода;
– сальдо накопленных денежных средств на начало первого подпериода; 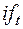 – величина притока денежных средств в
– величина притока денежных средств в  -м подпериоде;
-м подпериоде; 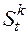 – сальдо накопленных денежных средств на конец
– сальдо накопленных денежных средств на конец  -го подпериода;
-го подпериода;  – допустимые остатки денежных активов на конец
– допустимые остатки денежных активов на конец  -го подпериода.
-го подпериода.
Целевая функция (2.19) содержит две группы слагаемых: первая группа отражает снижение потерь при «растягивании кредиторской задолженности»; вторая – нарастание штрафов из-за задержки платежей.
Ограничение (2.20) обеспечивает требуемую синхронизацию оттоков и притоков денежных средств.
Ограничение (2.21) отражает требование обязательности и однократности каждого платежа.
Использование коэффициентов наращения в выражениях (2.19) и (2.20) осуществляется с учётом приведения по времени денежных потоков внутри подпериода по принципу постнумерандо.
С учётом вероятностного характера притоков денежных средств  сальдо притоков
сальдо притоков 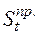 также представляет собой случайную величину:
также представляет собой случайную величину:
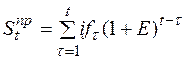 . (2.23)
. (2.23)
Используя результаты имитационного моделирования притоков денежных средств, можно получить значение сальдо притоков денежных средств, которое будет достигнуто или превышено с вероятностью 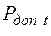 . С этой же вероятностью будет выполняться ограничение (2.20) при переходе от детерминированной к стохастической постановке задачи.
. С этой же вероятностью будет выполняться ограничение (2.20) при переходе от детерминированной к стохастической постановке задачи.
В качестве критерия эффективности рассматриваемой задачи, помимо минимизации потерь, могут использоваться: критерии минимизации колебаний сальдо накопленных денежных средств, критерий максимизации суммы свободных денежных средств к заданному сроку и т.д.
Метод решения поставленной задачи зависит от её размерности и особенностей. В качестве возможных методов могут быть использованы: метод полного перебора вариантов, метод направленного перебора вариантов на основе подхода «ветвей и границ» с учётом особенностей задачи и стандартные методы решения задач линейного программирования с булевыми переменными (Балаша, Гомори и др.).
Для решения поставленной задачи могут использоваться инструментальные средства WinQSB и Lindo. Последнее инструментальное средство позволяет решать модели, содержащие до 300 булевых переменных.
Дата добавления: 2016-02-04; просмотров: 895;
