Индицирование рентгенограммы вращения
Задача индицирования рентгенограмм вращения, снятых по одному из векторов a, b или c, состоит в определении только двух индексов интерференционных пятен. Мы уже говорили, что третий индекс интерференционного пятна равен номеру слоевой линии, на которой он находится. Допустим, что снимался кристалл кубической сингонии. Вращение осуществлялось вокруг оси a*. Тогда первый индекс всех интерференционных пятен известен: для нулевой слоевой линии он равен 0, для 1-ой слоевой линии первый индекс равен 1 и т.д. Таким образом, индицирование сводится к определению только индексов K и L.
Индексы интерференции каждого рефлекса нарентгенограмме вращения можно определить, зная величину вектора Hhkl обратной решетки и угол скольжения q.
Величина вектораHдля любого интерференционного пятна определяется из соотношения ½H½=1/d . Подставляя в эту формулу значение d из уравнения Вульфа-Брегга (2dsinq=l), получим
½H½= 
(5.7)
Для кубической сингонии (a=b=c):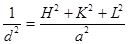 
= êH ê2,откуда
H2+K2+L2 = ( êHê/a*)2 = ( êHê× a )2 (5.8)
Для разных слоев рентгенограммы вращения:
0-слой (0, K, L) ( êHê× a)2 = K2+L2
1-ый слой (1, K, L) ( êHê× a)2 = K2+L2+1 или K2 + L2 = ( êHê× a)2 – 1
2-ой слой (2, K, L) ( êHê× a)2 = K2+L2+4 или K2 + L2 = ( êH ê× a)2 – 4
3- ий слой (3, K, L) ( êHê× a)2 = K2+L2+9 или K2 + L2 = ( êHê× a)2 – 9
(5.9)
Соотношение (5.9) позволяет вычислить сумму квадратов интересующих нас индексов K и L, что приемлемо для всех слоевых линий, если определен угол скольжения q.
Для нулевой слоевой линии расчет угла скольжения q рентгенограммы следующий: промеряем расстояние 2l между двумя симметричными пятнами нулевой слоевой линии и определяем угол отражения q по формуле (аналогично расчету дебаеграммы):
2q 0 =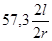 
(5.10)
где r – радиус цилиндрической камеры вращения. Далее отделяем пятна b-излучения (при съемке без фильтра), учитывая признаки b-отражений и используя соотношение
sin qa / sin qb = la / lb (5.11)
Для каждого пятна a-излучения вычисляем угол q°, абсолютную величину вектора H (5.7) и, воспользовавшись соотношением (5.9), определяем ( êH ê× a)2 как и недостающие индексы К, L .
Для пятен на n-слоевой линии вектор H не лежит в плоскости n-слоя обратной решетки (рис. 3.21). Поэтому определяем угол отражения q для пятен n-ой слоевой линии из прямоугольного сферического треугольника А Pn¢ P0 (рис.5.5), который является частью сферы с радиусом r.
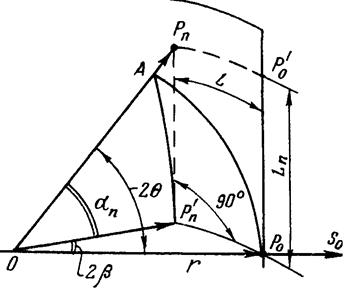
Рис.5.5. Определение угла скольжения q по положению пятен в n-слое.
cos 2q = cos 2b × cos an (5.12)
Угол an получаем из формулы (5.4). Для определения угла b имеем, как и в случае 0-слоя,
b=57,3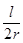 
(5.13)
где l – расстояние от средней линии симметрии рентгенограммы вращения P0P0¢ (рис.5.5) до интерференционного пятна Pn. Так как удобнее измерять расстояние между двумя симметричными пятнами на одной слоевой линии, то есть 2l, причем в данном случае ошибка сильно уменьшается, то формула для определения угла b
2b=57,3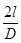 
(5.14)
Пятна от Ka-излучения для n-ой слоевой линии (n¹0) выявляются сразу, так как они лежат несколько ниже пятен Ka-излучения вдоль прямых, идущих от a-пятен к выходу первичного пучка (пятно в центре рентгенограммы).
Определив угол отражения q0 из (5.12), далее вычисляем для каждого пятна вектор H,( êHê× a)2 и индексы К и L.
Дата добавления: 2016-02-04; просмотров: 1134;