БЕЗМОМЕНТНАЯ ТЕОРИЯ РАСЧЁТА ОБОЛОЧЕК ВРАЩЕНИЯ
7.1. Условия безмоментного состояния оболочек
В инженерной практике в ряде случаев оказывается, что в оболочках вращения при определённых внешних воздействиях не возникают деформации изгиба поверхности и связанные с ними внутренние усилия в виде изгибающих и крутящих моментов. Условия, при которых наблюдаются эти состояния, нетрудно обосновать исходя из общей теории оболочек. В рассматриваемом разделе указанные условия объясняются простейшими физическими соображениями. В частности, ясно, что:
· при действии нагрузок, приложенных по касательной в любой точке поверхности оболочки, следует ожидать, что и внутренние усилия будут иметь то же направление и тем самым вызывать либо сжатие, либо растяжение произвольного элемента оболочки (рис. 7.1); если даже сосредоточенные нагрузки и действуют по нормали к поверхности, то безмоментное состояние возможно на достаточном удалении от них:
· конечно, и поверхность оболочки должна быть гладкой и непрерывной, без резких изломов, без скачкообразного изменения толщины (в общем случае - жёсткости), вследствие чего возникают деформации изгиба;
· на боковых гранях оболочки ничто не должно препятствовать перемещению кромок по нормали к поверхности оболочки, причём крепления опор должны обеспечивать сохранение формы оболочки при нагружении.
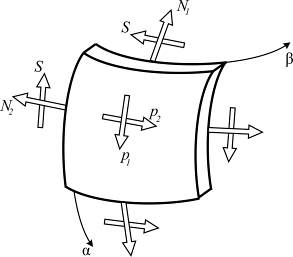
Рис. 7.1
Следует ожидать, что расчёт оболочек по безмоментной теории окажется проще расчёта по общей теории, когда указанные условия не соблюдаются и приходится принимать во внимание взаимовлияние нормальных усилий и моментов.
7.2. Общие уравнения безмоментной теории оболочек вращения
Вывод уравнений равновесия безмоментного состояния оболочек осуществляется на основе условий равновесия, полученных для общего случая (см. раздел 6). Как и ранее, при выводе уравнений необходимо рассмотреть бесконечно малый элемент оболочки  , вырезанный двумя парами нормальных плоскостей
, вырезанный двумя парами нормальных плоскостей  ,
,  , соответственно, и сформировать условия равновесия элемента при действии вектора нагрузки
, соответственно, и сформировать условия равновесия элемента при действии вектора нагрузки 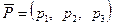 , составив сумы проекций усилий на оси сферической системы координат (рис. 7.2).
, составив сумы проекций усилий на оси сферической системы координат (рис. 7.2).
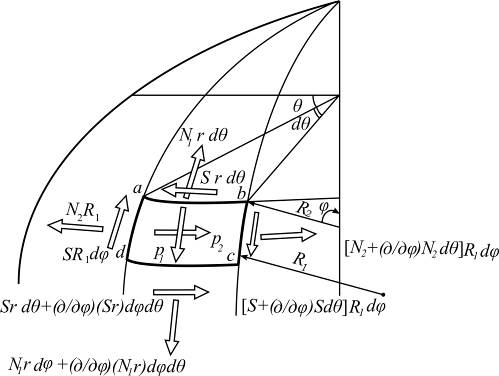
Рис. 7.2
При этих условиях расчёт оболочек выполняют по безмоментной теории, полагая изгибающие и крутящие моменты  ,
, 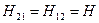 , а также поперечные силы
, а также поперечные силы  равными нулю, т.е. принимая изначально
равными нулю, т.е. принимая изначально
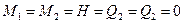 , (7.1)
, (7.1)
во всех уравнениях равновесия (6.20). На этом основании уравнения безмоментной теории оболочек при равенстве сдвигающих усилий 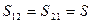 принимают вид:
принимают вид:
1. 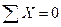 ,
, 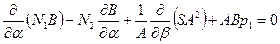 ,
,
2. 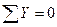 ,
, 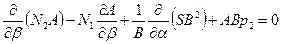 , (7.2)
, (7.2)
3. 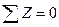 ,
, 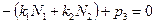 .
.
Остальные три условия в виде 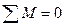 относительно осей координат удовлетворяются тождественно, поскольку моменты и поперечные силы
относительно осей координат удовлетворяются тождественно, поскольку моменты и поперечные силы 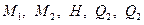 исключаются из рассмотрения. Таким образом, основными факторами напряженного состояния оболочки являются нормальные усилия
исключаются из рассмотрения. Таким образом, основными факторами напряженного состояния оболочки являются нормальные усилия 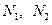 и сдвигающее усилие
и сдвигающее усилие 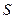 .
.
В дополнение к условиям равновесия (7.2) следует принять во внимание геометрические уравнения (см. раздел № 5):
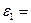
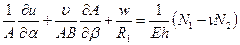 , (7.3,а)
, (7.3,а)
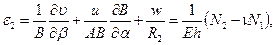 (7.3,б)
(7.3,б)
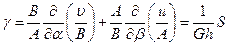 (7.3,в)
(7.3,в)
и физические соотношения (6.10).
7.3 Уравнения напряжённо-деформированного состояния безмоментных оболочек вращения
Уравнения состояния безмоментной теории оболочек вращения целесообразно записать в сферических координатах 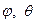 . В этом случае в уравнениях равновесия (7.2) следует принять:
. В этом случае в уравнениях равновесия (7.2) следует принять:
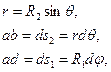 (7.4,а)
(7.4,а)
где 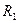 - радиус кривизны срединной поверхности вдоль меридиана,
- радиус кривизны срединной поверхности вдоль меридиана, 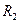 - расстояние от поверхности до оси вращения, измеряемое по нормали к поверхности (радиус кривизны в широтном направлении);
- расстояние от поверхности до оси вращения, измеряемое по нормали к поверхности (радиус кривизны в широтном направлении); 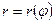 - радиус окружности, полученный в результате сечения оболочки плоскостью, перпендикулярной оси вращения. Следовательно, коэффициенты Ламе
- радиус окружности, полученный в результате сечения оболочки плоскостью, перпендикулярной оси вращения. Следовательно, коэффициенты Ламе
 (7.4,б)
(7.4,б)
в данном случае зависят только от угловой координаты 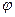 ; они не изменяются в широтном направлении (
; они не изменяются в широтном направлении (  ) вследствие симметрии поверхности.
) вследствие симметрии поверхности.
Формирование уравнений равновесия безмоментного состояния оболочек вращения осуществляется на основе условий равновесия (см. п. 7.2). При составлении условий равновесия следует принять во внимание равенства (7.4,а) и (7.4,б); в таком случае можно установить, что:
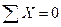 ,
, 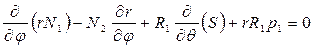 , (7.5,а)
, (7.5,а)
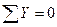 ,
,  , (7.5.б)
, (7.5.б)
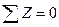 ,
, 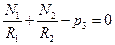 . (7.5,в)
. (7.5,в)
С помощью рис. 7.3 несложно определить проекцию дуги элемента на плоскость, перпендикулярную оси оболочки:
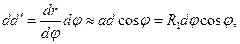
откуда находится производная
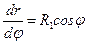 . (7.6)
. (7.6)
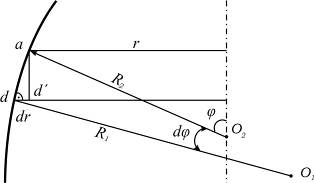
Рис. 7.3
С учётом определения (7.6) уравнения равновесия записываются в виде:
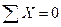 ,
, 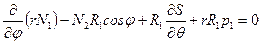 , (7.7,а)
, (7.7,а)
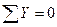 ,
, 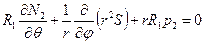 , (7.7,б)
, (7.7,б)
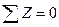 ,
, 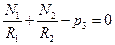 . (7.7,в)
. (7.7,в)
Точно также можно получить и геометрические уравнения в совокупности с физическими соотношениями:
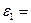
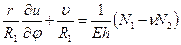 , (7.8,а)
, (7.8,а)
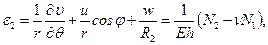 (7.8,б)
(7.8,б)
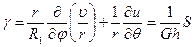 . (7.8,в)
. (7.8,в)
Очевидно, усилия 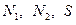 , как и перемещения
, как и перемещения 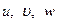 , являются функциями двух переменных
, являются функциями двух переменных 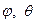 .
.
Интегрирование системы шести линейных дифференциальных уравнений (7.7), (7.8) безмоментной теории оболочек вращения начинается с решения системы трёх первых уравнений, поскольку задача определения усилий является, очевидно, статически определимой. После вычисления усилий переходят к интегрированию последних трёх уравнений. В результате чего находят и перемещения оболочки (см. рис. 7.2,б). Примеры расчёта оболочек на часто встречающиеся на практике виды нагрузок приводятся ниже.
7.4 Осесимметричные оболочки вращения
При действии нагрузки, симметричной относительно оси 0z, в уравнениях равновесия (7.7) производные по 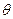 обращаются в нуль. Составляющая внешней нагрузки в широтном направлении также отсутствует (
обращаются в нуль. Составляющая внешней нагрузки в широтном направлении также отсутствует (  ). Если бы такая нагрузка действовала, то она приводила бы к возникновению скручивания оболочки, т.е. к появлению моментов
). Если бы такая нагрузка действовала, то она приводила бы к возникновению скручивания оболочки, т.е. к появлению моментов 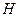 и сдвигающих сил
и сдвигающих сил 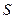 , что заведомо недопустимо. С учётом указанного допущения уравнение равновесия (7.7,б) удовлетворяется автоматически.
, что заведомо недопустимо. С учётом указанного допущения уравнение равновесия (7.7,б) удовлетворяется автоматически.
Два оставшихся уравнения несложно решить. Для этого из уравнения (7.7,в) необходимо выразить усилие 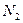 и подставить его в (7.7,а). В результате выводят уравнение
и подставить его в (7.7,а). В результате выводят уравнение
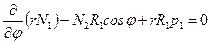 .
.
Умножив последнее на 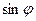 и приняв во внимание (7.3), находят
и приняв во внимание (7.3), находят
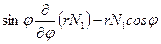
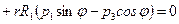 .
.
Подчёркнутые слагаемые можно привести к одному, воспользовавшись определением производной произведения 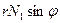 , а именно:
, а именно:
 .
.
В итоге уравнение равновесия оболочки вращения
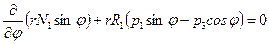
без труда интегрируется в общем виде
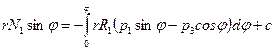 . (7.9)
. (7.9)
Постоянная интегрирования с, как всегда, определяется из граничного условия.
Вычислив усилие 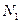 по (7.9), можно определить и другое -
по (7.9), можно определить и другое - 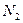 , воспользовавшись уравнением (7.7,в).
, воспользовавшись уравнением (7.7,в).
Для лучшего усвоения теории следует пояснить физический смысл интеграла (7.9). С этой целью достаточно умножить выражение (7.9) на 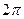
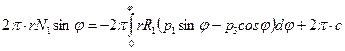 (*)
(*)
и заметить, что произведение 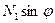 определяет вертикальную составляющую меридионального усилия
определяет вертикальную составляющую меридионального усилия 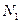 , действующего на уровне параллельного круга, соответствующем углу
, действующего на уровне параллельного круга, соответствующем углу 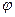 . Следовательно, величина
. Следовательно, величина 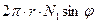 характеризует проекцию равнодействующую нормальных сил на уровне указанного круга (рис. 7.4).
характеризует проекцию равнодействующую нормальных сил на уровне указанного круга (рис. 7.4).
В правой части выражения (*), после внесения под знак интеграла множителя 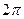 , можно установить, что величина
, можно установить, что величина
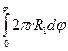
равна площади элементарного кольца, соответствующего бесконечно малому углу 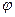 . Величины
. Величины 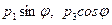 представляют собой проекции сил
представляют собой проекции сил  на вертикаль. Следовательно, подынтегральная функция является вертикальной составляющей нагрузки, действующей на элементарное кольцо. Тогда интеграл этой функции определяет полную вертикальную нагрузку, приходящуюся на оболочку с части поверхности, расположенной выше параллели, на уровне которой вычисляется меридиональное усилие
на вертикаль. Следовательно, подынтегральная функция является вертикальной составляющей нагрузки, действующей на элементарное кольцо. Тогда интеграл этой функции определяет полную вертикальную нагрузку, приходящуюся на оболочку с части поверхности, расположенной выше параллели, на уровне которой вычисляется меридиональное усилие 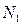 . Таким образом, выражение (7.9) можно считать условием равновесия рассматриваемой верхней части оболочки в виде
. Таким образом, выражение (7.9) можно считать условием равновесия рассматриваемой верхней части оболочки в виде 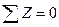 . Это даёт возможность найти постоянную интегрирования с.
. Это даёт возможность найти постоянную интегрирования с.
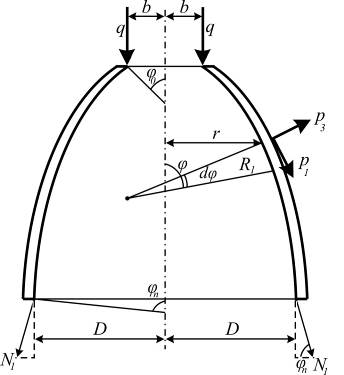
Рис. 7.4
Действительно, рассматривая, например, оболочку вращения, обладающую вырезом в верхней части на уровне угла 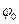 , и нагруженную на этой кромке равномерно распределённой нагрузкой
, и нагруженную на этой кромке равномерно распределённой нагрузкой  , легко определить равнодействующую этой нагрузки, равную
, легко определить равнодействующую этой нагрузки, равную 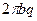 (здесь
(здесь 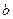 - радиус отверстия).
- радиус отверстия).
Составив условие равновесия рассматриваемой части
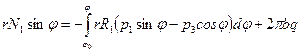 ,
,
без труда находят меридиональное усилие 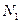 .
.
При отсутствии отверстия интеграл в правой части данного условия вычисляется в пределах от нуля до 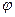 при значении
при значении 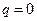 ; тогда
; тогда 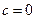 .
.
Значение окружного усилия находится согласно (7.7,в) по формуле
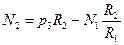 .
.
Пример 1. Расчёт сферического купола на действие собственного веса
Радиусы кривизн сферической оболочки в обоих направлениях одинаковы:
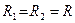 ,
,
где 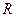 - радиус сферы (рис. 7.5,а). Текущий радиус
- радиус сферы (рис. 7.5,а). Текущий радиус 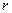 , входящий в уравнения состояния, равен
, входящий в уравнения состояния, равен
 .
.
Проекции вектора внешней нагрузки, каковой является собственный вес  , на оси координат, находятся без труда:
, на оси координат, находятся без труда:
 ,
, 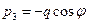 .
.
а б
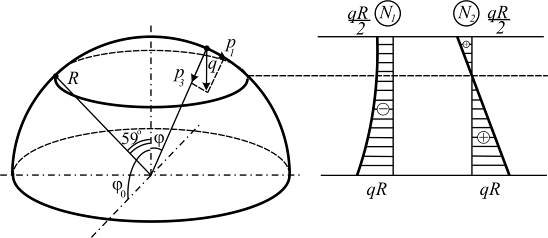
Рис. 7.5
C учётом этих данных, выражение (7.9) принимает вид
 ,
,
откуда
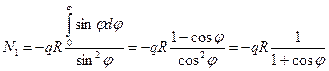 .
.
Окружное усилие
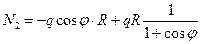 .
.
В вершине купола ( 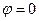 ) усилия находят по формуле
) усилия находят по формуле
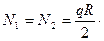
Характер изменения полученных усилий по высоте купола показан на рис. 7.5,б.
В отличие от усилия 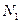 , значение
, значение 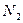 меняет знак на уровне горизонтальной плоскости, расположенной на широте
меняет знак на уровне горизонтальной плоскости, расположенной на широте 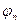 , положение которой легко найти из уравнения
, положение которой легко найти из уравнения 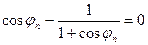 . Его решение даёт
. Его решение даёт 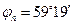 .
.
7.5 Примеры расчёта оболочек по безмоментной теории
А) Расчёт цилиндрических оболочек
Уравнения равновесия безмоментного состояния цилиндрической оболочки (рис. 7.6):
 (7.10,а)
(7.10,а)
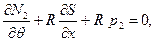 (7.10,б)
(7.10,б)
 (7.10,в)
(7.10,в)
несложно вывести из общих уравнений (7.2), зная параметры Ламе для круговой цилиндрической оболочки
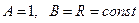 (7.11)
(7.11)
и радиусы кривизн 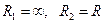 , где
, где 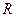 - радиус оболочки. Равенства (7.11) вытекают из определения квадрата длины линейного элемента цилиндрической поверхности (рис. 7.6)
- радиус оболочки. Равенства (7.11) вытекают из определения квадрата длины линейного элемента цилиндрической поверхности (рис. 7.6)
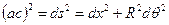 . (7.12)
. (7.12)
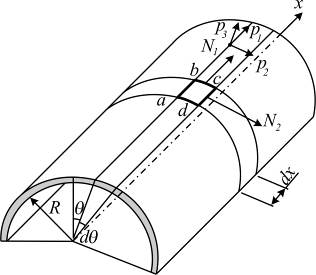
Рис. 7.6
Очевидно, окружное (кольцевое) усилие 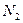 зависит только от нормального давления
зависит только от нормального давления 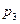 . Сдвигающее усилие определяется путём интегрирования (7.10,б):
. Сдвигающее усилие определяется путём интегрирования (7.10,б):
 . (7.13)
. (7.13)
Подобным образом находят и усилие
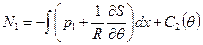 . (7.14)
. (7.14)
Геометрические уравнения для этого состояния оболочки выводят из соотношений (7.3) с учётом равенств (7.11), заменяя при этом 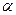 на
на 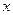 , а
, а 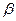 на
на 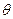 ; в сочетании с физическими зависимостями они принимают вид:
; в сочетании с физическими зависимостями они принимают вид:
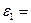
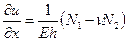 , (7.15,а)
, (7.15,а)
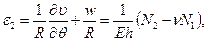 (7.15,б)
(7.15,б)
 . (7.15,в)
. (7.15,в)
Проекции вектора произвольной внешней нагрузки могут быть разложены в ряды Фурье:
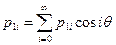 ,
,
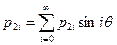 ,
,
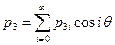 ,
,
где  ,
, 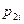 ,
, 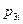 - известные кэффициенты, зависящие только от х.
- известные кэффициенты, зависящие только от х.
Далее достаточно найти решение задачи для одного из членов ряда, например, n – ого. Обладая им, несложно получить полное решение для всей совокупности членов ряда путём суммирования отдельных решений.
Из последнего условия  системы уравнений (7.10) следует, что окружное усилие
системы уравнений (7.10) следует, что окружное усилие 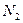 зависит только от внешнего давления, направленного по нормали к поверхности оболочки
зависит только от внешнего давления, направленного по нормали к поверхности оболочки
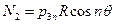 .
.
Дифференцируя это выражение по 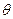 и подставляя производную в уравнение (7.10,б), находят сначала
и подставляя производную в уравнение (7.10,б), находят сначала
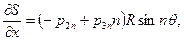
откуда
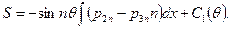
Вычислив производную 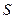 по
по 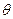 и подставив её в выражение (7.14), можно определить усилие и вдоль образующей цилиндра:
и подставив её в выражение (7.14), можно определить усилие и вдоль образующей цилиндра:
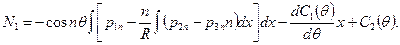
При отсутствии нагрузки вдоль образующей, т. е. при 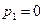 и постоянных (но, не равных) значениях
и постоянных (но, не равных) значениях 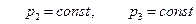 , выражения для усилий приобретают замкнутую форму. Для вывода формул величины
, выражения для усилий приобретают замкнутую форму. Для вывода формул величины  можно принять периодическими и полагать
можно принять периодическими и полагать
 ,
,
где 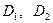 - произвольные постоянные. В таком случае усилия равны:
- произвольные постоянные. В таком случае усилия равны:
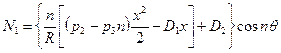 ,
,

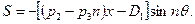
Постоянные интегрирования 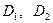 , как и функции
, как и функции  , и находятся из граничных условий.
, и находятся из граничных условий.
Б) Расчёт сферических оболочек на
на действие ветровых нагрузок
Действие ветровой нагрузки в первом приближении достаточно охарактеризовать единственной проекцией вектора внешней нагрузки, направленной по нормали к поверхности
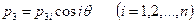 , (7.16)
, (7.16)
где 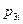 - функция распределения нагрузки, зависящая от координаты х в цилиндрической системе координат или от
- функция распределения нагрузки, зависящая от координаты х в цилиндрической системе координат или от 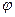 - в сферической.
- в сферической.
Следует обратить внимание на то, что данная функция, характеризующая нагрузку, при 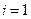 является неуравновешенной (рис. 7.7,а), в то время как при иных (целых) коэффициентах она самоуравновешена (рис. 7.7,б).
является неуравновешенной (рис. 7.7,а), в то время как при иных (целых) коэффициентах она самоуравновешена (рис. 7.7,б).
а б
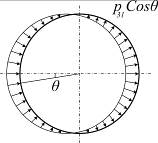
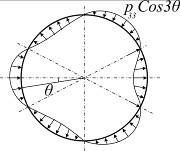
Рис. 7.7
В соответствии с принятым распределением нагрузки следует ожидать, что и усилия  будут функциями только одной переменной -
будут функциями только одной переменной - 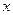 или
или 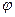 :
:
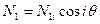 ,
,
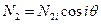 ,
,
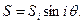
Подставив эти усилия в условия равновесия (7.8):
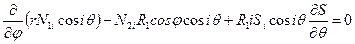 ,
,
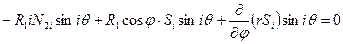 ,
,
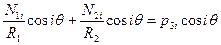
и сократив затем первое и третье условия на 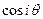 , а второе - на
, а второе - на 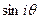 , приходят к уравнениям, не содержащим переменной
, приходят к уравнениям, не содержащим переменной 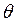 .
.
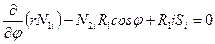 , (7.17,а)
, (7.17,а)
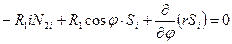 , (7.17,б)
, (7.17,б)
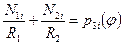 . (7.17,в)
. (7.17,в)
А это означает, что рассматриваемые усилия не зависят от координаты 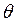 .
.
Известно, что система трёх уравнений состояния (7.17) произвольной оболочки вращения имеет общее решение, основу которого составляет некоторая «функция напряжений».
Ограничиваясь решением частной задачи, имеющей практическое значение, а именно случаем ветровой нагрузки  , направленной по нормали к сферической поверхности, усилия в оболочке можно определить, не прибегая к функции напряжений.
, направленной по нормали к сферической поверхности, усилия в оболочке можно определить, не прибегая к функции напряжений.
Действительно, из последнего уравнения системы (7.17) легко выразить усилие
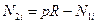 . (7.18)
. (7.18)
Подставив его в два других уравнения системы и поделив на 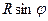 , можно установить систему:
, можно установить систему:
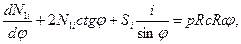

Структура данной системы такова, что при сложении уравнений
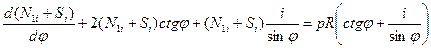 ,
,
а затем и вычитании

она распадается на два независимых дифференциальных уравнения первого порядка. Если обозначить:
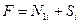 , (7.19,а)
, (7.19,а)
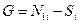 , (7.19,б)
, (7.19,б)
то уравнения предстанут в компактной форме:
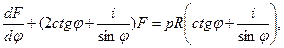 (7.20,а)
(7.20,а)
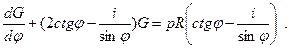 (7.20,б)
(7.20,б)
Для интегрирования любого из них применяется следующий подход. Задавшись, например, решением первого уравнения в виде произведения двух функций
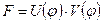 (7.21)
(7.21)
и определив производную этого произведения
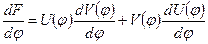 ,
,
само уравнение можно будет записать в виде
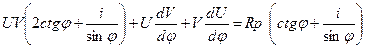 .
.
Данное уравнение удовлетворяется тождественно, если функции 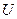 ,
, 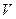 связаны соотношениями:
связаны соотношениями:
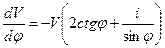 ,
,
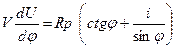 .
.
Интеграл первого из этих уравнений имеет аналитический вид
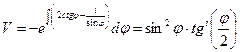 ,
,
в чём легко убедиться путём дифференцирования данного выражения. Второе уравнение интегрируется по аналогии с первым и также может быть записано в замкнутой форме
 .
.
Таким образом, в соответствии с (7.21) решение первого уравнения системы (7.20) принимает вид
 .
.
По аналогии с ним находят и решение второго уравнения системы.
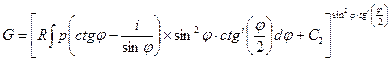 .
.
Усилия в оболочке 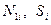 определяют на основе полученных выражений согласно (7.19).
определяют на основе полученных выражений согласно (7.19).
Дата добавления: 2015-12-16; просмотров: 10010;
