Метод средневзвешенных критериев

Метод средневзвешенных критериевявляется эффективным для оценки экспертами ряда альтернатив и вариантов слабо структурированных решений. Система взвешенных критериев может быть применена для оценки поставщиков продукции. На первом этапе экспертами дается оценка непосредственно критериев выбора. Предположим, цена за материал, размер минимальных поставок и т.д. Все критерии «взвешиваются» по отношению к главному критерию (См.:таблица 2). По выбранным взвешенным критериям оцениваются все возможные варианты решений. Допустим, четыре фирмы-поставщики продукции: А, Б, В, Г. На самом деле их может быть значительно больше. На этом этапе производится сравнительная оценка каждой фирмы по каждому критерию (См.:таблица 2).

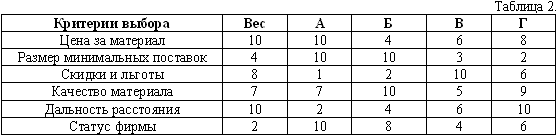
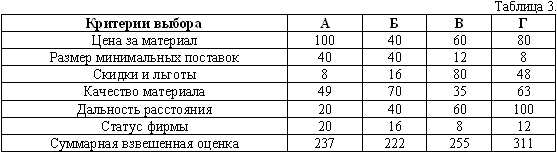
На последнем этапе определяется суммарное взвешивание вариантов с учетом разной «весовой» категории каждого критерия, т.е. перемножаются весовые показатели критериев выбора на взвешенные варианты по каждой строке (См.: таблица 3). Суммарная взвешенная оценка показывает наиболее адекватную оценку фирм-поставщиков.

Основные методы социологических исследований: определение выборочной совокупности, опрос респондентов, интервью, анкетирование.

В менеджменте методы социологических исследований применяются для изучения проблем в функциональной подсистеме управления персоналом, исследования мотивации, удовлетворенности работников трудом, организационной культуры, способов усовершенствования организации труда, вопросов социальной ответственности бизнеса, отслеживания любых характеристик, связанных с социальными параметрами системы управления.

Виды социологических исследований: контент-анализ, аналитическое исследование, экспресс-анализ, пилотажное исследование, экспертный опрос.

Определение выборки в социологических исследованиях может проводится разными методами.

1. По формуле:

2. n = 1¹ / (δ² +1/N), где

3. δ — доверительный интервал допустимой ошибки, как правило берется в пределах 5 %.

4. N — генеральная совокупность

5. n — выборочная совокупность

6. По формуле:

7. n = δ²t¹ /Δ², где n — выборочная совокупность

8. δ — дисперсия (степень однородности исследуемых единиц наблюдения)

9. t — коэффициент доверия (заданная точность)

10. Δ — предельная ошибка выборки.

11. Квотным методом. Берется 10 % единиц наблюдения генеральной совокупности.

12. Посредством определения статистических серий, т.е. однородных групп (гнезд).

Типы выборок

1. Квотная выборка — модель структуры генеральной совокупности, которая строится в виде квот (пропорций) распределения признаков изучаемых объектов.

2. Гнездовая выборка — метод выделения в генеральной совокупности однородных групп (гнезд), имеющих схожие признаки. Серии, попавшие в выборку, могут подвергаться сплошному или выборочному обследованию.

3. Шаговая выборка — систематическая случайная выборка, элементы которой отображены через какой-то определенный интервал исходного списка.

4. Простая случайная выборка — выборка, формируемая из элементов генеральной совокупности, совпадающих с номерами из таблицы случайных чисел.

5. Стихийная выборка — выборка, при которой критерии не задаются, практически опрос «первого встречного».

Тестирование как метод психологической диагностики находит широкое применение в исследовании систем управления персоналом. Тестирование применяется для стандартизированного измерения индивидуальных различий работников при отборе персонала, профессиональном обучении. Валидность тестового компонента теста — показатель, характеризующий его способность устойчиво различать профессиональную компетентность испытуемых. Высоковалидный компонент фиксирует высокий балл у более подготовленных испытуемых и низкий — у менее подготовленных.

Параметрический метод исследования систем управления основывается на количественном выражении исследуемых свойств системы и установления зависимости между рядом параметров. Обычно выделяют функциональные и корреляционные зависимости. Корреляционные в отличие от функциональных являются неполными и искажаются влиянием посторонних факторов. В случае функциональной связи коэффициент корреляции равен 1. Корреляционный метод применяется в производстве для разработки разного рода нормативов, анализе спроса и предложения. Простейшим видом корреляционного уравнения, характеризующего взаимосвязь между двумя параметрами, является уравнение прямой:

Y = a + bX,

Где Х,Y — независимая и зависимая переменные,

a,b — постоянные коэффициенты.

Примером линейной зависимости может быть объем реализации Y от объема произведенной на предприятии продукции X. Вывод о прямолинейном характере зависимости можно проверить путем простого сопоставления данных и регистрацией их в прямоугольной системе координат. Важной задачей является определение постоянных коэффициентов связи между переменными параметрами, которые наилучшим образом отвечают значениям X,Y. В данном примере, факторы влияющие на объемы производства и реализации продукции. Величина исследуемого параметра довольно часто складывается под влиянием не одного, а нескольких факторов. Поэтому можно использовать линейное уравнение множественной корреляции.

Факторный анализ состоит в переходе от первоначального описания исследуемых объектов, заданных совокупностью большого числа непосредственно измеряемых признаков, к описанию наиболее значимых компонентов, отражающих наиболее существенные свойства явления. Эти главные компоненты содержат большую часть информации, заключенной в первоначальных переменных Х и объясняют большую часть их полной дисперсии. Такого рода переменные, называемые факторами, являются функциями исходных признаков. Для определения переменных, имеющих наибольшие факторные нагрузки, применяется расчет дисперсии, а также определяется вклад компонента в полную дисперсию. Переменные при использовании факторного анализа не подразделяются априорно на зависимые и независимые и рассматриваются как равноправные. В этом его отличие от параметрического метода, при котором берутся взаимозависимые переменные.