Гауссов волновой пакет.

Рассмотрим начальную волновую функцию следующего вида.

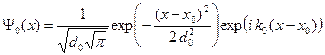(B.33)

Физический смысл параметров x₀, d₀ и k₀ будет выяснен далее.

Найдем распределение плотности вероятности в начальный момент времени. Это распределение определяется следующей формулой:

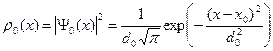. (B.34)

График этого распределения приведен на Рис.1. Как видно, пакет имеет гауссов характер. Центр пакета находится в точке с координатой x_m=x₀. Полуширина пакет равна d₀. Амплитуда пакета определяется следующей формулой:

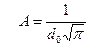(B.35)

Убедимся, что начальная волновая функция (B.33) нормирована на единицу. Действительно подставив (B.33) в условие нормировки (B.7), получаем единицу.

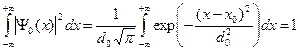(B.36)

Выясним, чему равен импульс электрона в состоянии с волной функцией (B.33).

Квантовая механика утверждает, что частица имеет определенный импульс в состоянии, волновая функция которого является собственной функцией оператора импульса.

Выяснить является ли волновая функция собственной функцией оператора импульса очень просто. Надо проверить удовлетворяет ли эта функция следующему уравнению:

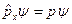. (B.37)

Здесь оператор проекции импульса на ось x в координатном представлении имеет вид:

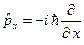, (B.38)

а p является импульсом частицы.

Берем волновую функцию (B.33) и подставляем ее в уравнение (B.37). Оказывается волновая функция (B.33) не удовлетворяет уравнению (B.37). Значит электрон в состоянии с волновой функцией (B.33), не имеет определенного импульса.

Так как электрон в состоянии с волновой функцией (B.33), не имеет определенного импульса, то можно говорить только о среднем значении импульса электрона p₀.

Квантовая механика утверждает, что среднее значение физической величины f в состоянии с волновой функцией Y(x,t) определяется с помощью следующего выражения:

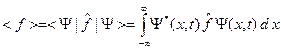(B.39)

Здесь 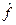– оператор соответствующий физической величине f.

Применим формулу (B.39) для нахождения среднего значения импульса электрона в состоянии с волновой функцией (B.33). Подставляем оператор импульса (B.38) в формулу (B.39) и получаем следующее выражение:

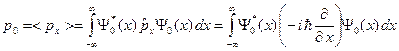. (B.40)

Подстановка волновой функции (B.33) в формулу (B.40) и интегрирование дает следующий результат:

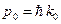(B.41)

Таким образом, параметр k₀ в волновой функции (B.33) связан со средним значением импульса соотношением (B.41). Можно считать, что k₀– это среднее волновое число гауссова пакета (B.33).

Кроме среднего значения импульса, можно говорить о вероятности обнаружения того или иного значения импульса у электрона в состоянии с волновой функцией (B.33). Рассмотрим, как можно вычислить эту вероятность.

Из курса квантовой механики известно, что собственная функция оператора проекции импульса на ось x равна следующему выражению:

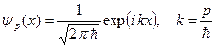. (B.42)

Отметим что собственная функция оператора импульса (B.42) нормирована на d-функцию:

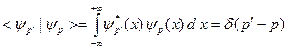. (B.43)

Произвольную волновую функцию Y(x) представляем в виде разложения по собственным функциям импульса:

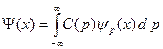. (B.44)

Коэффициенты C(p) в разложении (B.44) вычисляются по следующей формуле:

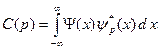. (B.45)

Квантовая механика утверждает, что плотность вероятности обнаружить импульс p у электрона в состоянии с волновой функцией Y(x) равна:

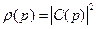(B.46)

Возьмем начальную волновую функцию (B.33) и собственную функцию импульса (B.39) и подставим их в формулу (B.45). Получаем следующее выражение:

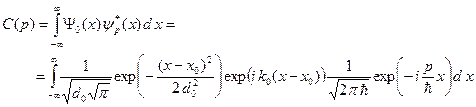. (B.47)

Вычисление интеграла (B.47) дает следующий результат:

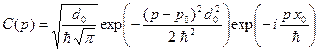. (B.48)

Используя формулы (B.46), (B.48) получаем следующее выражение для плотности вероятности импульса электрона в состоянии (B.33):

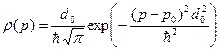(B.49)

График этого распределения приведен на Рис.4.

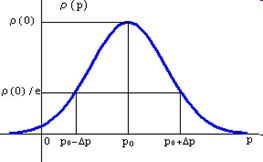
Рис.4.

Распределение плотности вероятности импульса электрона в гауссовом волновом пакете.

Здесь амплитуда распределения r(0) и полуширина распределения Dp определяются следующими выражениями:

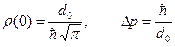(B.50)

Максимум распределения (B.49) приходится на значение p₀ равное среднему значению импульса.

Убедимся, что распределение импульса (B.49) нормировано на единицу. Действительно, записав условие нормировки, получаем следующий результат:

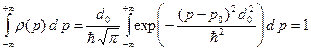. (B.51)

Найдем дисперсию распределения импульса. Используя распределение (B.49) получаем следующий результат:

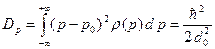(B.52)

Тогда среднеквадратичное отклонение импульса от среднего значения будет равно следующей величине:

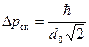(B.53)

Найдем дисперсию распределения координаты электрона в волновом пакете. Используя распределение (B.34) получаем следующий результат:

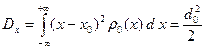(B.54)

Тогда среднеквадратичное отклонение координаты будет равно следующей величине:

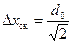(B.55)

В квантовой механике показывается, что принцип неопределенности Гейзенберга, записанный для среднеквадратичных отклонений импульса и координаты, имеет следующее математическое выражение:

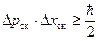(B.56)

Соотношение Гейзенберга (B.56) имеет место для состояний с произвольной волновой функцией. Для волновой функции в виде гауссово волнового пакета (B.33) соотношение неопределенности (B.56) принимает следующий вид:

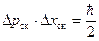(B.57)

Поэтому для волнового пакета (B.33) неравенство Гейзенберга превращается в равенство. Если написать соотношение Гейзенберга для полуширины волнового пакета d₀ и для полуширины распределения по импульсу Dp, то соотношение Гейзенберга примет следующий вид:

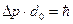(B.58)

Как уже говорилось выше электрон, состояние которого описывается волновым пакетом, не имеет определенной энергии. Можно только говорить о вероятности электрону иметь ту или иную энергию. Найдем для электрона распределение плотности вероятности энергии 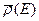. Для этого используем обычные правила квантовый механики. Волновую функцию электрона разложим по собственным функциям оператора Гамильтона для свободного движения частицы. Полная система собственных функций 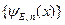имеет следующий вид.

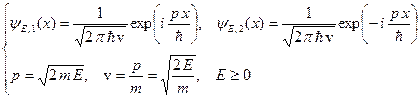(B.59)

Здесь собственная функция 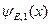соответствует электрону, который имеет энергию E, импульс p и движется в положительную сторону оси x. Аналогично, собственная функция 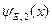соответствует электрону, который имеет энергию E, импульс p и движется в отрицательную сторону оси x. Собственные функции (B.59) нормированы на d-функцию от энергии следующим образом.

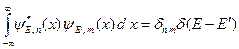(B.60)

Раскладываем произвольную волновую функцию 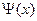электрона по полной системе собственных функций (B.59).

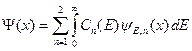(B.61)

Коэффициенты 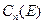в разложении (B.61) вычисляются по следующей формуле:

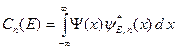. (B.62)

Причем величина 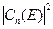равна плотности вероятности того, что электрон может находиться в состоянии с функцией 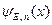. В этом случае коэффициенты 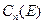должны быть нормированы на вероятность равную единице. Действительно, для коэффициентов 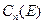имеет место следующая формула.

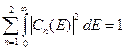(B.63)

Плотность вероятности 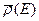того, что электрон при свободном движении будет иметь ту или иную энергию E, определяться следующей формулой.

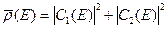(B.64)

Здесь учтено, что электрон с заданной энергией E и импульсом p может двигаться как в положительном направлении оси x, так и в отрицательном направлении.

Пусть волновая функция электрона является гауссовым волновым пакетом (B.33). Подставляем в формулу (B.62) вместо волновой функции 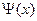волновую функцию (B.33), интегрируем и затем результат подставляем в формулу (B.64). В результате для плотности вероятности 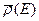получаем следующую формулу.

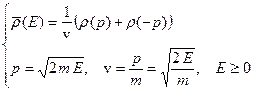(B.65)

Здесь плотность 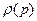вероятности импульса электрона, которая вычисляется по формуле (B.49). Вероятность электрону иметь энергию в заданном интервале 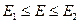определяется следующим интегралом.

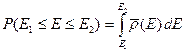(B.66)

Учитывая структуру формулы (B.65) удобно в интеграле (B.66) перейти от интегрирования по энергии к интегрированию по импульсу. В результате получим следующую формулу для вычисления вероятности.

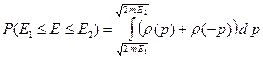(B.67)

Среднюю энергию 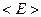электрона в состоянии с волновой функцией в виде волнового пакета (B.33) можно найти двумя способами. Во-первых, можно использовать формулы теории вероятности. В этом случае среднее значение находится по следующей формуле.

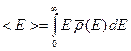(B.68)

Во-вторых, среднее значение энергии можно получить, используя правила квантовой механики. Отметим, что средняя энергия одновременно будет средней кинетической энергией, потому что потенциальная энергия равна нулю для свободного движения. Применяем формулу (B.39) для нахождения средней энергии электрона в состоянии с волновой функцией (B.33) и получаем следующее выражение:

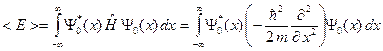(B.69)

Подстановка волновой функции (B.33) в формулу (B.69) и интегрирование дает следующий результат:

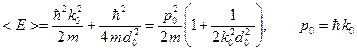(B.70)

Заметим, что энергия электрона 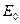, которая приводится в вариантах, не совпадает со средней энергией электрона. Действительно, для энергии 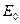используется следующая формула.

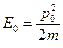(B.71)