Стационарные решения уравнения Шредингера.
Приложение A.
Нахождение решения уравнения Шредингера для свободного электрона в виде волнового пакета.
Запишем уравнение Шредингера для свободного электрона
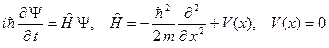(A.1)
После преобразований уравнение Шредингера принимает вид
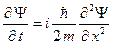(A.2)
Это уравнение решаем с начальным условием
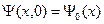(A.3)
Здесь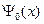 
- волновая функция электрона в начальный момент времени. Ищем решение уравнения (A.2) в виде интеграла Фурье
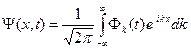(A.4)
Подставляем (A.4) в (A.2) и получаем
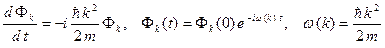(A.5)
Решение (A.4) можно теперь записать в следующем виде
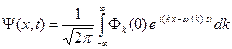(A.6)
Используем начальное условие (A.3), и из (A.6) получаем разложение начальной волновой функции электрона в интеграл Фурье.
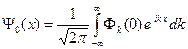(A.7)
К выражению (A.7) применяем обратное преобразование Фурье
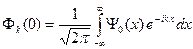(A.8)
Подведем итог проделанным преобразованиям. Итак, если известна волновая функция электрона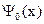 
в начальный момент времени, то после интегрирования (A.8) находим коэффициенты 
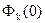. Затем после подстановки этих коэффициентов в (A.6) и интегрировании, получаем волновую функцию электрона 
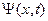в произвольный момент времени в любой точке пространства.
Для некоторых распределений 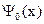интегрирование можно провести в явном виде и получить аналитическое выражение для решения уравнения Шредингера. В качестве начальной волновой функции возьмем распределение Гаусса, модулированное плоской монохроматической волной.
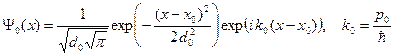(A.9)
Здесь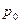 
- средний импульс электрона. Выбор начальной волновой функции в таком виде позволят получить решение уравнения Шредингера в виде волнового пакета.
Рассмотрим подробно свойства начальной волновой функции (A.9).
Во-первых, волновая функция нормирована на единицу.
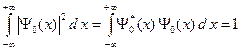(A.10)
Нормировка (A.10) легко доказывается, если использовать следующий табличный интеграл.
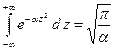(A.11)
Во-вторых, если волновая функция нормирована на единицу, то квадрат модуля волновой функции является плотностью вероятности, нахождения электрона в данной точке пространства.
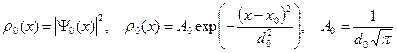(A.12)
Здесь величину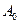 
будем называть амплитудой волнового пакета в начальный момент времени. Физический смысл амплитуды пакета – это максимальное значение распределения вероятности. На Рис.1 показан график распределения плотности вероятности.
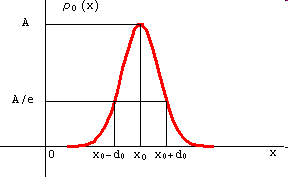
Рис.1.
Распределение плотности вероятности в начальный момент времени.
Отметим некоторые особенности графика на Рис.1.
1. Координата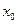 
– это точка на оси x, в которой распределение вероятности имеет максимальное значение. Поэтому можно сказать, что с наибольшей вероятностью можно обнаружить электрон вблизи точки .
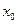2. Величина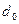 
определят отклонение от точки 
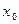, при котором величина распределения уменьшается в e раз по сравнению с максимальным значением.
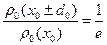(A.13)
В этом случае величину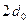 
называют шириной волнового пакета в начальный момент времени, а величину 
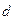– полушириной пакета.
3. Вычислим вероятность нахождения электрона в интервале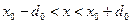 
.
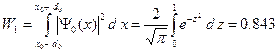(A.14)
Таким образом, вероятность обнаружить электрон в области с центром 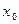и полушириной 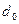равна 0.843. Эта вероятность близка к единице, поэтому обычно, об области с полушириной 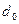говорят, как об области, где находится электрон в начальный момент времени.
В-третьих, начальная волновая функция 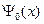не является собственной функцией оператора импульса 
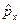. Поэтому электрон в состоянии с волновой функцией 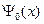не имеет определенного импульса, можно говорить только о среднем импульсе электрона. Вычислим средний импульс электрона.
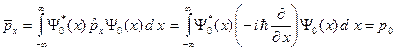(A.15)
Поэтому, величина 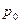в формуле (A.9) является средним значением импульса электрона. Формула (A.15) легко доказывается, если использовать табличный интеграл (A.11).
Таким образом, свойства начальной волновой функции разобраны. Теперь подставим функцию 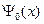в интеграл Фурье (A.8) и найдем коэффициенты .
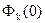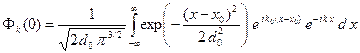(A.16)
В интеграле (A.16) делаем следующую замену переменной интегрирования.
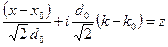(A.17)
В результате интеграл (A.16) принимает следующий вид.
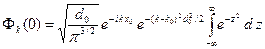(A.18)
В результате получаем следующее выражение для коэффициентов .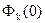
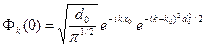(A.18)
Подставляем коэффициенты в формулу (A.6), получаем следующее интегральное выражение для волновой функции.
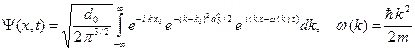(A.19)
В интеграле (A.19) делаем следующую замену переменной интегрирования.
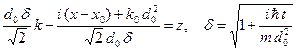(A.20)
В результате интеграл (A.19) принимает следующий вид.
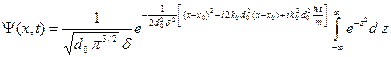(A.21)
Окончательно получаем формулу для волнового пакета.
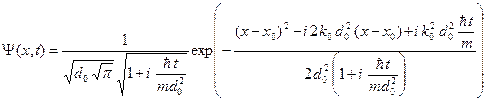(A.22)
Легко видеть, что для начального момента времени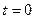 
формула (A.22) переходит в формулу (A.9) для начальной волновой функции. Найдем плотность вероятности для функции (A.22).
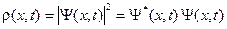(A.23)
Подставляем волновой пакет (A.22) в формулу (A.23), и в результате получаем следующее выражение.
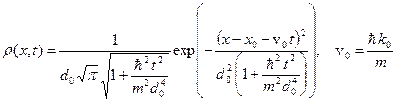(A.24)
Здесь центр волнового пакета, или максимум распределения плотности вероятности, движется со скоростью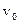 
, равной следующей величине.
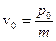(A.25)
Полуширина волнового пакета увеличивается со временем, и определятся следующей формулой.
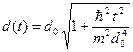(A.26)
Амплитуда волнового пакета уменьшается со временем, и определятся следующей формулой.
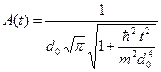(A.27)
Таким образом, распределение вероятности для волнового пакета можно записать в следующем виде.
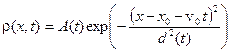(A.28)
На Рис.2. показано распределение вероятности в три последовательных момента времени.
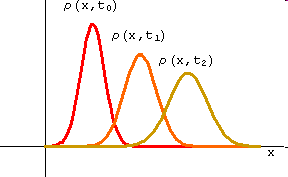
Рис.2.
Распределение вероятности в три последовательных момента времени.
Приложение B.
Общие сведения о решении уравнения Шредингера.
Введение.
Движение квантовой частицы в общем случае описывается уравнением Шредингера:
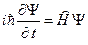. (B.1)
Здесь i – мнимая единица, h =1.0546´10-34 (Дж×с) - постоянная Планка. Оператор Ĥ называется оператором Гамильтона. Вид оператора Гамильтона зависит от типа взаимодействия электрона с внешними полями.
Если не учитывать спиновые свойства электрона, например, не рассматривать движение электрона в магнитном поле, то оператор Гамильтона можно представить в виде.
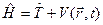(B.2)
Здесь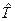 
– оператор кинетической энергии:
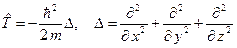, (B.3)
где m=9.1094´10-31 (кг) – масса электрона. Потенциальная энергия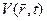 
описывает взаимодействие электрона с внешним электрическим полем.
В данной лабораторной работе будет рассматриваться одномерное движение электрона вдоль оси x. Уравнение Шредингера в этом случае принимает следующий вид:
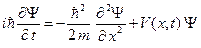. (B.4)
Уравнение (B.4) с математической точки зрения является дифференциальным уравнение в частных производных для неизвестной волновой функции Y=Y(x,t). Известно, что такое уравнение имеет определенное решение, если заданы соответствующие начальные и граничные условия. Начальные и граничные условия выбираются исходя из конкретной физической задачи.
Пусть, например, электрон движется слева направо с некоторым средним импульсом p0. Кроме того, в начальный момент времени t=0, электрон локализован в некоторой области пространства xm-d < x < xm+d. Здесь xm – центр области локализации электрона, а d – эффективная полуширина этой области.
В этом случае начальное условие будет выглядеть следующим образом:
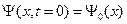. (B.5)
Здесь Y0(x) – волновая функция в начальный момент времени. Волновая функция это комплексная функция, поэтому графически удобно представлять не саму волновую функцию, а плотность вероятности.
Плотность вероятности, нахождения электрона в данном месте в данный момент времени выражается через волновую функцию следующим образом:
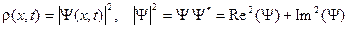. (B.6)
Заметим, что вероятности должна быть нормирована на единицу. Отсюда получаем условие нормировки волновой функции:
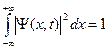. (B.7)
Распределение плотности вероятности в начальный момент времени
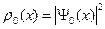, (B.8)
можно изобразить графически. На Рис.3. показано возможное расположение электрона в начальный момент времени.
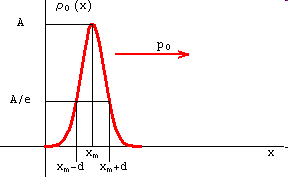
Рис.3.
Расположение электрона в момент t=0.
Из этого рисунка видно, что с наибольшей вероятностью электрон находится в точке xm. Буквой A будем обозначать амплитуду (максимальное значение) распределения вероятности. Из этого рисунка так же видно, как определяется ширина 2d или полуширина d распределения. Если распределение имеет экспоненциальный или гауссов характер, то ширину распределения определяют на уровне в e раз меньшем, чем максимальное значение.
На Рис.3. показан вектор среднего импульса электрона. Это означает, что электрон движется справа налево, и распределение вероятности так же будет перемещаться справа налево. На Рис.2. показано распределение вероятности в три последовательных момента времени. На Рис.2. видно, что максимум распределения xm(t) перемещается слева направо.
На Рис.2. можно заметить, что движение электрона справа налево сопровождается деформацией распределения плотности вероятности. Амплитуда A(t) уменьшается, а полуширина d(t) растет. Все указанные детали движения электрона можно получить, если решить уравнение Шредингера (B4) с начальным условием (B.5).
Резюме. В зависимости от постановки физической задачи может меняться вид уравнения Шредингера. При исследовании тех или иных физических явлений, описываемых уравнением Шредингера, выбираются нужные начальные и граничные условия для нахождения решения уравнения Шредингера.
Стационарные решения уравнения Шредингера.
Если электрон движется в постоянном по времени внешнем поле, то его потенциальная энергия не будет зависеть от времени. В этом случае одним из возможных решений уравнения Шредингера (B.4) является решение с разделяющимися переменными по времени t и по координате x.
Применяем известный в математике прием решения дифференциальных уравнений. Ищем решение уравнения (B.4) в виде:
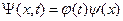. (B.9)
Подставляем (B.9) в уравнение (B.4) и получаем следующие соотношения:
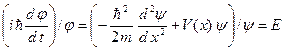. (B.10)
Здесь E – константа, которой в квантовой механике придается смысл полной энергии электрона. Соотношения (B.10) эквивалентны следующим двум дифференциальным уравнениям:
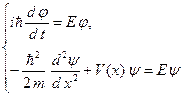. (B.11)
Первое уравнение в системе (B.11) имеет следующее общее решение:
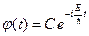. (B.12)
Здесь C – произвольная константа. Подставляем (B.12) в выражение (B.9) и получаем решение уравнения Шредингера (B.4) в виде:
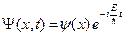, (B.13)
где функция y(x) удовлетворяет уравнению.
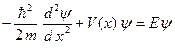(B.14)
Константа C содержится в функции y(x).
Решение уравнения Шредингера (B.4) в виде выражения (B.13), называется стационарным решением уравнения Шредингера. Уравнение (B.14) называют стационарным уравнение Шредингера. Функцию y(x) называют волновой функцией, независящей от времени.
Состояние электрона, которое описывается волной функцией (B.13), называется стационарным состоянием. В квантовой механике утверждается, что в стационарном состоянии электрон обладает определенной энергией E.
Полученные результаты можно обобщить на уравнение Шредингера (B.1) для трехмерного движения электрона. Если оператор Гамильтона Ĥ не зависит явно от времени, то одним из возможных решений уравнения Шредингера (B.1) является стационарное решение следующего вида:
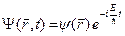, (B.15)
где волновая функция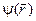 
удовлетворяет стационарному уравнению Шредингера.
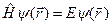(B.16)
Заметим, что уравнения (B.14) и (B.16) в квантовой механике имеют еще оно название. Эти уравнения являются уравнениями на собственные функции и собственные значения оператора Гамильтона. Другими словами, решая уравнение (B.16) находят энергии E (собственные значения оператора Гамильтона) и соответствующие им волновые функции 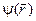(собственные функции оператора Гамильтона).
Резюме. Стационарные решения уравнения Шредингера являются некоторым классом решений из огромного множества других решений уравнения Шредингера. Стационарные решения существуют, если оператор Гамильтона не зависит явно от времени. В стационарном состоянии электрон имеет определенную энергию. Для нахождения возможных значений энергии надо решить стационарное уравнение Шредингера.
Волновой пакет.
Легко видеть, что стационарные решения уравнения Шредингера не описывают движение локализованного электрона, как показано на Рис.1 и Рис.2. Действительно, если взять стационарное решение (B.13) и найти распределение вероятности, то получится функция независящая от времени.
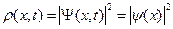(B.17)
В этом нет ничего удивительного, стационарное решение (B.13) является одним из возможных решений дифференциального уравнения в частных производных (B.4).
Но вот что интересно, в силу линейности уравнения Шредингера (B.4) относительно волновой функции Y(x,t), для решений этого уравнения выполняется принцип суперпозиции. Для стационарных состояний этот принцип утверждает следующее. Любая линейная комбинация стационарных решений (с разными энергиями E) уравнения Шредингера (B.4) то же является решением уравнения Шредингера (B.4).
Чтобы дать математическое выражение для принципа суперпозиции, нужно сказать несколько слов об энергетическом спектре электрона. Если решение стационарного уравнения Шредингера (B.14) имеет дискретный спектр, то это означает, что уравнение (B.14) можно записать в следующем виде:
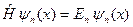(B.18)
где индекс n пробегает, вообще говоря, бесконечный ряд значений n=0,1,2,¼ . В этом случае решение уравнения Шредингера (B.4) можно представить в виде суммы стационарных решений.
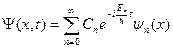(B.19)
В квантовой механике доказывается, что собственные функции yn(x) дискретного спектра можно сделать ортонормированной системой функций. Это означает, что выполняется следующее условие нормировки.
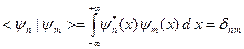(B.20)
Здесь dn m– символ Кронекера.
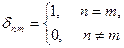
Так вот, если система функций yn(x) ортонормированная, то коэффициенты Cn в сумме (B.19) имеют простой физический смысл. Квадрат модуля от коэффициента Cn равен вероятности того, что электрон в состоянии с волновой функцией (B.19) имеет энергию En.
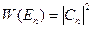(B.21)
Самое главное в этом утверждении, что электрон в состоянии с волновой функцией (B.19) не имеет определенной энергии. При измерении энергии, у этого электрона может быть получена любая энергия из набора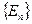 
с вероятностью (B.21).
Поэтому говорят, что электрон может обладать той или иной энергией с вероятностью, определяемой формулой (B.21).
Электрон, который находится в стационарном состоянии и имеет определенную энергию, будем называть монохроматическим электроном. Электрон, который не находится в стационарном состоянии, и поэтому не имеет определенной энергии, будем называть немонохроматическим электроном.
Если решение стационарного уравнения Шредингера (B.14) имеет непрерывный спектр, то это означает, что уравнение (B.14) можно записать в следующем виде:
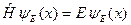, (B.22)
где энергия E принимает значения на некотором непрерывном интервале [Emin, Emax]. В этом случае решение уравнения Шредингера (B.4) можно представить в виде интеграла стационарных решений.
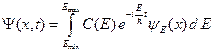(B.23)
Собственные функции непрерывного спектра yE(x) в квантовой механике принято нормировать на d-функцию:
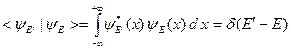, (B.24)
Определение d-функции содержится в следующих интегральных соотношениях:
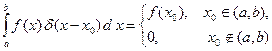
Чтобы наглядно представить поведение d-функции, приводят следующее описание этой функции:
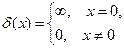
Так вот, если система функций yE(x) нормирована на d-функцию, то квадрат модуля от коэффициента C(E) в интеграле (B.23) равен плотности вероятности того, что электрон в состоянии с волновой функцией (B.19) имеет энергию E.
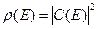(B.25)
Волновая функция Y(x,t) представленная в виде суммы (B.19) или в виде интеграла (B.23) от стационарных решений уравнения Шредингера, называется волновым пакетом.
Таким образом, состояние не монохроматического электрона описывается волновым пакетом. Можно сказать еще так, в состояние немонохроматического электрона дают вклад состояния монохроматического электрона со своими весовыми множителями.
На Рис.1. и Рис.2. изображены волновые пакеты электрона в разные моменты времени.
Резюме. Состояние немонохроматического электрона описывается волновым пакетом. Немонохроматический электрон не обладает определенной энергией. Волновой пакет можно представить суммой или интегралом волновых функций стационарных состояний со своими энергиями. Вероятность того, что немонохроматический электрон имеет ту или иную энергию из этого набора энергий, определятся вкладом соответствующих стационарных состояний в волновой пакет.
Свободное движение. Общее решение уравнения Шредингера.
В зависимости от поля, с которым взаимодействует электрон, решение стационарного уравнения Шредингера (B.14) может иметь разный вид. В данной лабораторной работе рассматривается свободное движение. Поэтому в уравнении (B.14) положим потенциальную энергию равной нулю. В результате получим следующее уравнение:
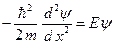, (B.26)
общее решение этого уравнения имеет следующий вид:
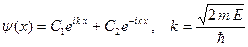. (B.27)
Здесь C1 и С2 - две произвольные константы, k имеет смысл волнового числа.
Теперь с помощью выражения (B.23) запишем общее решение уравнения Шредингера для свободного движения. Подставляем функцию (B.27) в интеграл (B.23). При этом учитываем, что пределы интегрирования по энергии E для свободного движения выбираются от нуля до бесконечности. В результате получаем следующее выражение:
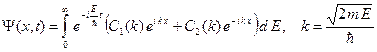(B.28)
В этом интеграле удобно перейти от интегрирования по энергии E к интегрированию по волновому числу k. Будем считать, что волновое число может принимать как положительные, так и отрицательные значения. Для удобства введем частоту w, связанную с энергией E, следующим соотношением:
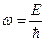. (B.29)
Преобразуя интеграл (B.28), получаем следующее выражение для волнового пакета:
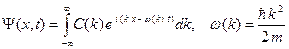. (B.30)
Интеграл (B.30) дает общее решение уравнения Шредингера (B.4) для свободного движения. Коэффициенты C(k) находятся из начальных условий.
Возьмем начальное условие (B.5) и подставим туда решение (B.30). В результате получим следующее выражение:
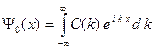(B.31)
Интеграл (B.31) есть не что иное, как разложение начальной волновой функции в интеграл Фурье. Используя обратное преобразование Фурье, находим коэффициенты C(k).
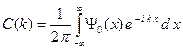. (B.32)
Резюме. Под свободным движением электрона понимается движение в отсутствии внешнего поля в бесконечной области пространства. Если известна волновая функция электрона в начальный момент времени Y0(x), то с помощью формул (B.32) и (B.30) можно найти общее решение уравнения Шредингера Y(x,t) для свободного движения электрона.
Дата добавления: 2015-12-01; просмотров: 4225;