Теоретическая оценка влияния адсорбции на запасённую энергию в скелете породы

В нулевом приближении минералы породы можно представить как совокупность малых сфер. Каждая сфера за счет адсорбции флюида на ее поверхности будет расширяться под действием собственных сил упругости и изменять свой объём. Для отдельной частицы можно записать известные соотношения:

βdp = 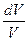(3.14)

и

р = , (3.15)

где: β - сжимаемость твердого тела;

w – удельная поверхностная энергия сферы;

r - радиус твердой частицы;

р - избыточное давление, возникающее из –за кривизны поверхности;

V– объем частицы.

Дифференцируя (3.15), получим

dp = 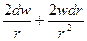(3.16)

Из (3.14) и (3.16) после совместного решения получим

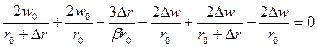- (3.17)

При условии Δr « r из (3.17) получим соотношение между относительным изменением объема минерала и изменением его удельной поверхностной энергии:

ε_v = 3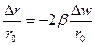

Расширение породы будет тем больше, чем значительней изменение Δw.

В том случае, когда расширение минералов несущего скелета происходит в условиях действия горного давления, порода приобретает запас энергии. Именно эта запасённая энергия расходуется на упорядоченное движение флюида в поровых каналах и теплоперенос в минералах породы.

Что касается расклинивающего давления, то оно, по – видимому, во многих случаях будет превалирующим в процессе накопления породой запасенной энергии. Однако, оценка такой энергии связана с принципиальными трудностями.