разомкнутой цепи звеньев
Логарифмические частотные характеристики имеют большое практическое значение. Поэтому рассмотрим их построение. В общем случае частотные характеристики строят по методике, изложенной в разделе 3.1. Однако часто результирующую передаточную функцию смешанного соединения звеньев можно свести к виду
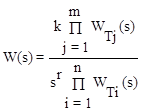, (3.54)
где WT(s) - передаточная функция типового звена.
В этом случае построение ЛАХ производится по выражению
L(w) = 20lgA(w) = 20lg|W(jw)|=
= 20lgk - r´20lgw +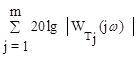 
- 
.
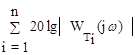Построение ЛФХ производится по выражению
y(w) = argW(jw) = -r´900 +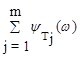 
- 
.
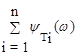Таким образом, результирующая ЛАХ определяется суммированием ЛАХ составляющих типовых звеньев, а результирующая ЛФХ - соответственно суммированием ЛФХ составляющих типовых звеньев. Таблицы характеристик типовых звеньев имеются в литературе [1,7].
Асимптотические ЛАХ можно построить непосредственно по виду передаточной функции (3.54) по следующему правилу, состоящему из четырех пунктов.
1. Частотная область разбивается на диапазоны, границы которых определяются сопрягающими частотами, соответствующими постоянным времени передаточной функции:
.
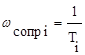Число сопрягающих частот равняется числу постоянных времени в передаточной функции, а число частотных диапазонов на единицу больше.
2. Первая низкочастотная асимптота ЛАХ, которая проводится в крайнем левом низкочастотном диапазоне, имеет наклон -(20´r)дб/дек и проходит через точку с координатами: w=1 с-1, L(1)=20lg k дб, где r - показатель степени оператора Лапласа s, записанного в знаменателе передаточной функции (3.54).
3. На сопрягающих частотах ЛАХ претерпевает изломы.
3.1. Если сопрягающая частота соответствует постоянной времени Тi, находящейся в знаменателе передаточной функции, то ЛАХ делает излом вниз на -(20´v)дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Тi.
3.2. Если сопрягающая частота соответствует постоянной времени Тi, находящейся в числителе передаточной функции, то ЛАХ делает излом вверх на +(20´v) дб/дек, где v - порядок типового динамического звена, в которое входит эта постоянная времени Тi.
4. Вторая асимптота проводится до следующей сопрягающей частоты и так далее.
Пример. Построить ЛАХ звена, имеющего следующую передаточную функцию: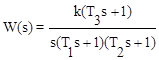 
,
где k = 100 с-1 ; Т1= 5 с; Т2= 0.01 с; Т3= 0.5 с.
Решение.
1. Представим передаточную функцию, как комбинацию типовых звеньев:
.
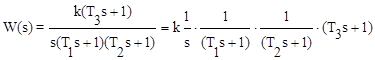2. Находим сопрягающие частоты:
wсопр1= 1/Т1= 0.2 с-1; wсопр2= 1/Т2= 100 с-1; wсопр3= 1/Т2= 2 с-1.
3. Строим ЛАХ.
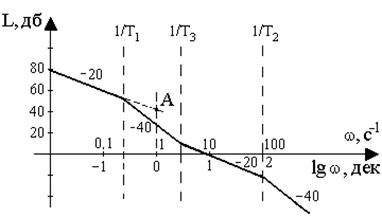
Рис. 3.13. Логарифмическая частотная характеристика звена
3.1. Частотную область разбиваем на четыре диапазона.
3.2. Низкочастотный участок ЛАХ имеет наклон
-(20´r)= -(20´1)= -20дб/дек и проходит через точку с координатами: w = 1с-1, L(1) = 20lg k= 40дб (точка А[1,40]).
3.3. На частоте 1/Т1 ЛАХ делает излом вниз на
-(20´v)= -(20´1)= -20 дб/дек.
3.4. На частоте 1/Т3 ЛАХ делает излом вверх на
(20´v) = (20´1) = 20дб/дек.
3.5. На частоте 1/Т2 ЛАХ делает излом вниз на
-(20´v) = -(20´1) = -20 дб/дек.
Вид полученной ЛАХ приведен на рис. 3.13.
Используя то же правило, по ЛАХ звена можно однозначно определить передаточную функцию.
Пример.Определить передаточную функцию звена, ЛАХ которого имеет вид, представленный на рис. 3.14.
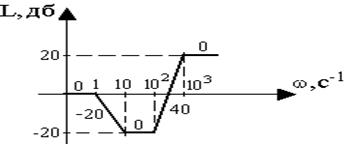
Рис. 3.14. ЛАХ звена
Решение. Передаточная функция имеет вид
,
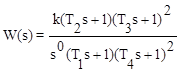где k=10L(1)/20=100=1 с-1;
Т1= 1 с; Т2= 0.1 с; Т3= 0.01 с; Т4= 0.001 с.
При более сложных формах передаточной функции W(s), например, при наличии внутренних обратных связей, построение ЛАХ усложняется. Однако часто можно и сложные выражения приводить к аналогичному виду (3.54), разложив на множители многочлены числителя и знаменателя.
Дата добавления: 2016-02-02; просмотров: 628;