НА НЕУСТАНОВИВШИХСЯ РЕЖИМАХ ФИЛЬТРАЦИИ
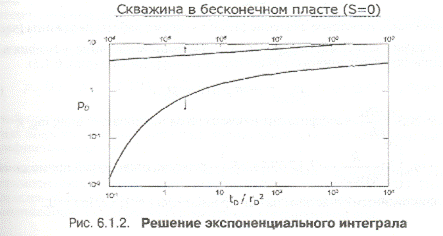
Решение линейного стока определяется функцией Ei(x), которая представлена в виде табличных значений. Исследования показали, что при х < 0,01 экспоненциальный интеграл можно достаточно точно аппроксимировать простой логарифмической функцией (рис. 6.1.2):
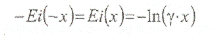(6.1.2)
где g = 1.781 - постоянная Эйлера.
Т.е. общее аналитическое решение представляется в безразмерном виде:
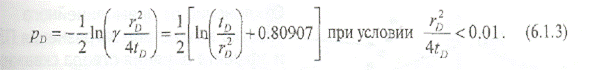
Данное условие практически всегда выполняется в случае замера давления в скважине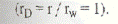 
Решение линейного стока в размерном виде:
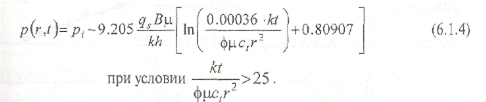
Решение линейного стока в размерном виде для rD = 1, с учетом скин-эффекта:
|
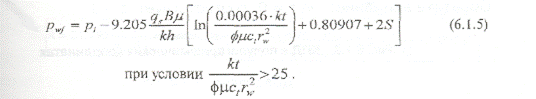
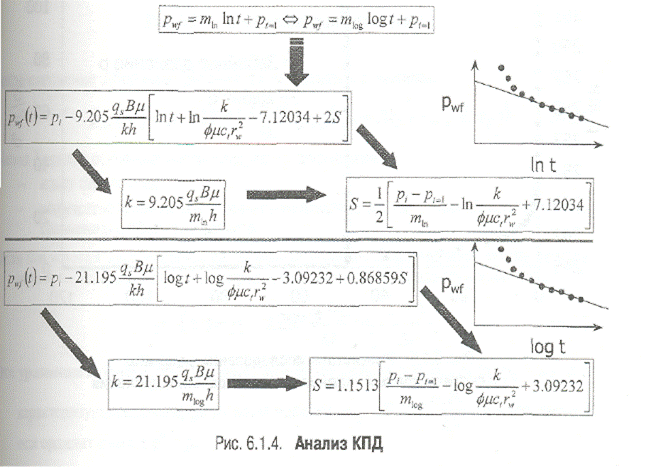
Использование натурального логарифма In t при анализе данных КПД (рис. 6.1.4).
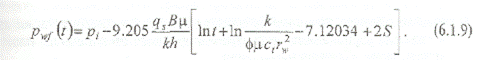
При выполнении интерпретации данных "вручную" используют обычную миллиметровую бумагу для построения графика зависимости pwf от In t; данный подход наиболее удобен при анализе данных с использованием процедуры линейной регрессии методом наименьших квадратов. Натуральный логарифм лежит в основе всей теории анализа данных КПД, и уравнения, выведенные на его основе, имеют более простую форму.
Использование десятичного логарифма log t при анализе данных КПД (рис, 6.1.4).
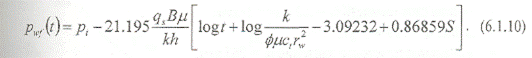
Данный подход, построение полулогарифмического графика зависимости pwf от log t, был широко распространен в прошлом, когда для этого использовалась полулогарифмическая бумага.
Очень важно: замеренные данные на начальном периоде испытаний отклоняются от прямолинейного участка, это вызвано ВСС и загрязнением ПЗП. Поэтому при определении pt=1 необходимо брать значение, отсекаемое экстраполированным прямолинейным участком на вертикальной координатной оси.
Упражнение 1 – КПД
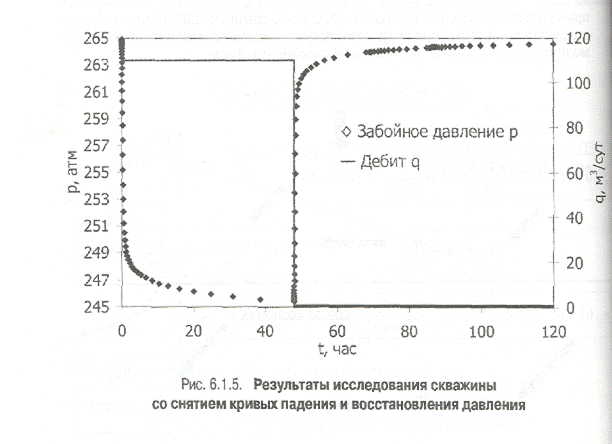
В качестве примера приведем фрагмент обработки и интерпретации данных ГДИС. Скважина располагается в центре однородного бесконечного пласта, давление! пласте выше давления насыщения.
ИСХОДНЫЕ ДАННЫЕ по скважине:
пористость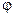 
= 0.2;
продуктивная толщина h = 80 м;
радиус скважины rw = 0.08 м;
объемный коэффициент нефти В0 = 1;
вязкость нефти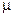 
= 1 спз;
общая сжимаемость ct = 2.2 х 10-4 1/атм;
дебит q=110м3/сут;
начальное пластовое давление р =265 атм.
МЕТОД ХОРНЕРА
Если скважина работала определенный период времени tp с дебитом q, а давление замерялось после остановки скважины в периоды времени Dt, то забойное давление после закрытия скважины можно определить, используя принцип суперпозиции, т.е. суммируя изменения забойного давления для дебитов (рис. 6.2.1):q в период времени (tp + Dt) и (О-q) в период времени Dt.
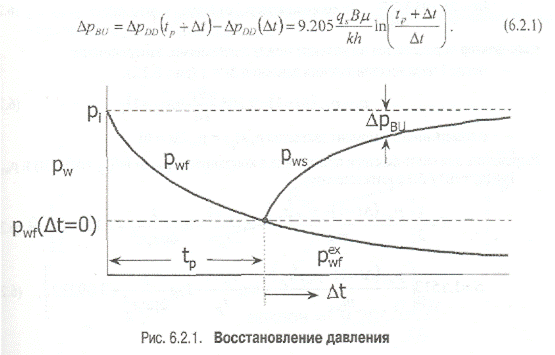
Тогда изменение забойного давления после закрытия скважины:
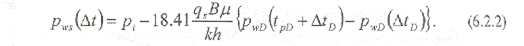
Метод Хорнера основывается на следующих допущениях:
- пласт бесконечен;
- количество флюида, извлеченного из пласта за время tp, пренебрежимо мало по сравнению с объемами запасов.
Если эти условия удовлетворяются, то можно заменить безразмерное давление в уравнении на логарифмическую аппроксимацию экспоненциального интеграла:
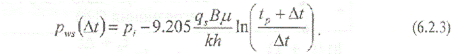
Это уравнение Хорнера, описывающее линейную зависимость pws от In [(tp +Dt)/Dt] и характеризующееся коэффициентом наклона
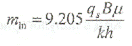
и пересечением оси ординат в точке
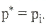
kh вычисляется по величине наклона m (рис. 6.2.2) прямолинейного участка КВД в полулогарифмических координатах (аналогично процедуре анализа данных КПД):
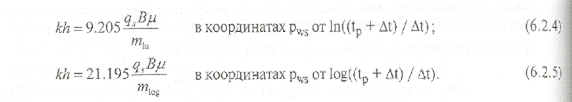
скин-фактор определяется по разнице между давлениями, замеренными:
- после 1 часа восстановления давления Dt = 1 (рис. 6.2.2):
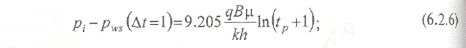
- и измеренного в момент закрытия pwf{tp) = pws(Dt = 0).
Выражение для скин-фактора примет вид в координатах pws от ln((tp +Dt) / Dt) и pws от log((tp + Dt) / Dt) соответственно:
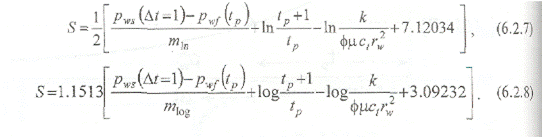
Прямолинейный участок на графике Хорнера можно экстраполировать до времени (tp + Dt) / Dt = 1, соответствующего бесконечному времени остановки скважины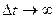 
(рис. 6.2.3). В конечном счете давление восстановится до значения первоначального давления пласта р* = pj; в случае незначительного истощения в период добычи. Данный способ достаточно точен только в случае короткого периода добычи, когда объем добытого флюида незначителен по сравнению с общими запасами в пласте. Обычно эти условия выполняются при проведении гидродинамических испытаний на разведочных скважинах.
В случае, если значительное количество флюида уже было извлечено из пласта за время tp, то экстраполированное давление р* можно использовать для оценки среднего пластового давления. В данном случае р* отличается от среднего пластового давления, и необходимо скорректировать это значение, используя известный МВН метод (Matthews-Brons-Hazerbroek).
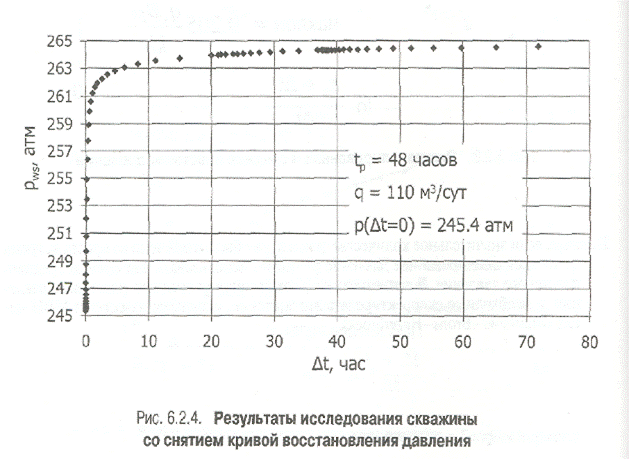
Упражнение 2 - КВД
В качестве примера обработки и интерпретации данных по восстановлению давления воспользуемся данными из упражнения 1, Скважину, которая проработала с постоянным дебитом q период времени tp, закрыли на 72 часа и замеряли забойное давление pws. Скважина располагается в центре однородного бесконечного пласта, давление в пласте выше давления насыщения.
ИСХОДНЫЕ ДАННЫЕ по скважине:
пористость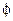 
= 0.2;
продуктивная толщина h = 80 м;
радиус скважины rw - 0.08 м;
объемный коэффициент нефти В0 = 1;
вязкость нефти 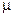= 1 спз;
общая сжимаемость ct = 2.2 х 10-4 1/атм;
время работы скважины tp = 48 час;
дебит q = 110 м3/сут;
забойное давление в момент закрытия скважины р(D1=0) = 245.4 атм.
MDH МЕТОД
На графике Хорнера КВД имеет линейную зависимость от ln[(tp + Dt) / Dt]. Уравнение Хорнера можно записать в более простой форме, в случае, если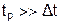 
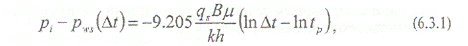
т.е. забойное давление изменяется линейно в зависимости от In Dt. Данный метод интерпретации данных КВД был разработан с участием Миллера, Дайса и Хэтчинсона.
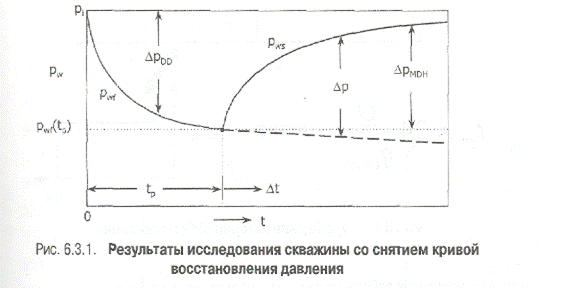
Разница между значениями Dр и DpMDH мала при 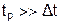(рис. 6.3.1), т.е:
- в начальный период времени проведения исследования скважины методом восстановления давления;
- после достаточно долгого периода добычи с постоянным дебитом.
При интерпретации данных КВД с помощью MDH метода строится график зависимости DpMDH от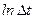 
и по наклону m прямолинейного участка кривой определяются параметрыпласта:
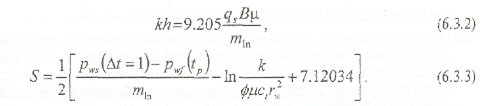
Простота данного метода является одним из основных его преимуществ, однако существует несколько недостатков данного метода:
- данный метод невозможно использовать для нахождения экстраполированного давления р*;
- данный метод можно корректно использовать только в случае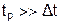
Дата добавления: 2015-12-01; просмотров: 7961;