ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ

Производная в ГДИС - логарифмическая производная давления Р'.

Датчик давления записывает дискретные значения давления P_j в определенные моменты времени t_i. Для того, чтобы построить график производной давления, необходимо найти значение производной в каждой точке t_i :

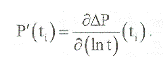
Производная давления может быть получена с помощью численного дифференцирования и понятия «конечной разности».

Различают три вида конечных разностей;

Центральная конечная разность имеет порядок точности выше порядка точности левой и правой конечных разностей.

Чтобы посчитать значение логарифмической производной, необходимо составить таблицу со значениями In t_i и P_i и по формуле конечной разности подсчитать значение производной в каждой точке t_i{табл. 5.3.1).

Процесс дифференцирования данных усиливает шум, присущий данным (рис. 5.3.1).

Непосредственное дифференцирование может дать очень зашумленную производную. поэтому необходимо сглаживать данные

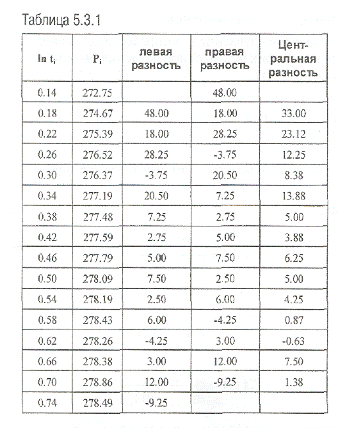
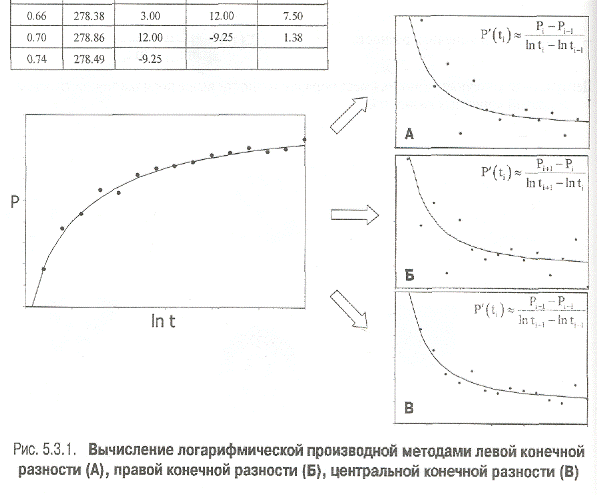
Существует множество алгоритмов сглаживания данных.

В основе этих алгоритмов лежит понятие интервала дифференцирования .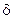

Для того, чтобы найти значение производной в точке t_i;, рассматривают интервал [In t_i-d; lnt_i;+ d].

К наиболее распространенным алгоритмам сглаживания данных относятся:

· Многоточечная регрессия.

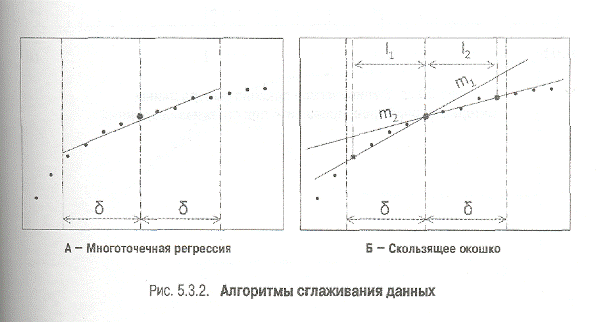
Через точки, попавшие в интервал [In t_i-d; lnt_i;+ d] проводится регрессионная прямая. Наклон это прямой линии есть значение производной в точке t_i (рис. 5.3.2. Б).

· Скользящее окошко.

Через точки (In t_i-d) и In t_i проводят прямую линию, определяют ее наклон m₁. Через точки (In t_i)и (In t_i-d)) проводят прямую линию, определяют ее наклон m₂. Производная в точке t_i есть среднее арифметическое наклонов m₁ и m₂. В общем случае, если точки расположены неравномерно по времени, прямые строятся через точку t_i и самые дальние от нее точки, попадающие в интервал [In t_i-d; lnt_i;+ d]. В данном случае производная равна средневзвешенному наклонов m₁ и m₂ (обозначения см. на рис. 5.3.2. Б):

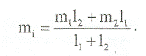
При сглаживании данных необходимо всегда помнить, что «чрезмерное» сглаживание может привести к потере информации.

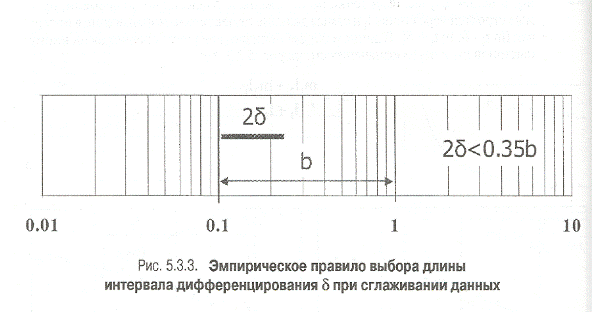
Существует эмпирическое правило выбора длины интервала дифференцирования d:

2d должно быть не больше 0.35 длины логарифмического цикла (рис. 5.3,3).

Это правило основано на наблюдении того факта, что все переходные режимы течения длятся не меньше, чем 2/3 длины логарифмического цикла.

Использование максимального значения интервала сглаживания допустимо лишь в случае чрезвычайно зашумленных данных.

АНАЛИЗ ДАННЫХ