СВОЙСТВА ПРОИЗВОДНОЙ

Безразмерное давление для исследования по КПД для радиального притока выглядит следующим образом:

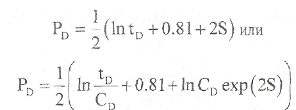
Тогда логарифмическая производная давления для радиального притока равна:

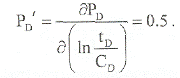
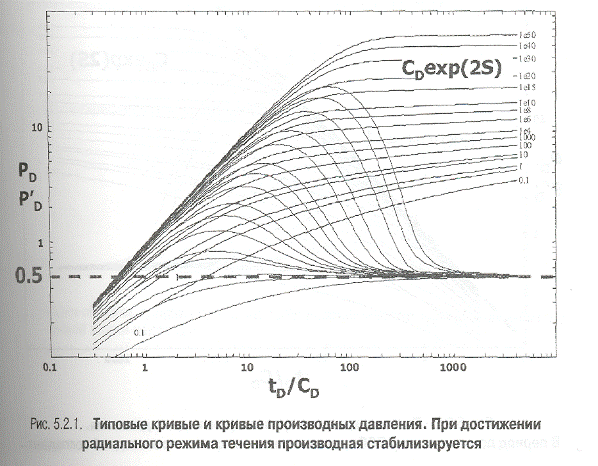
Значит, участки кривых производных, относящиеся к радиальному притоку, представляют собой горизонтальные прямые линии с ординатой равной 0,5 (в безразмерных координатах) (рис. 5.2.1).

Вообще говоря, любой режим течения описывается либо логарифмической зависимостью давления от времени, либо степенной зависимостью.

В случае логарифмической зависимости (радиальный, полурадиальный и т.д. режимы течения):

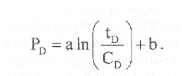
Значит, логарифмическая производная равна:

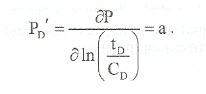
Таким образом, график производной в данном случае имеет вид горизонтальной прямой.

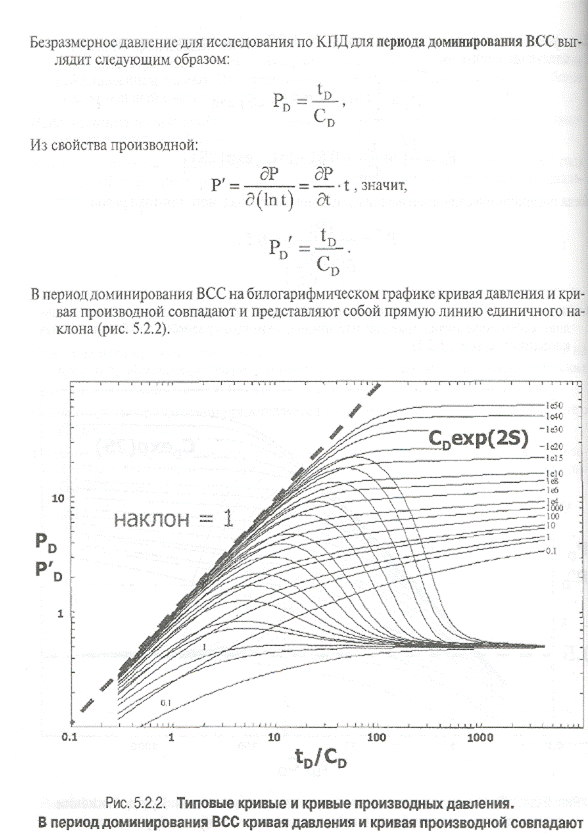
В случае степенной зависимости (ВСС; линейный, билинейный, сферический, псевдоустановившийся режимы течения):

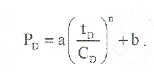
Значит, логарифмическая производная равна:

и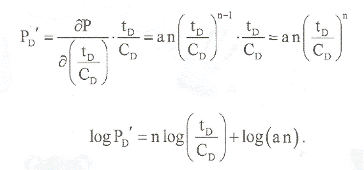

Таким образом, график производной в билогарифмических координатах имеет вид прямой линии наклона n.

Итак, так как любой режим течения описывается либо логарифмической зависимостью давления от времени, либо степенной зависимостью, на графике производной каждый режим течения имеет свой характеристический признак (прямую линию определенного угла наклона).

В англоязычной литературе часто характеристические признаки (тангенсы угла наклона прямолинейных участков производной) называют "fingerprints", что дословно переводится как "отпечатки пальцев". Подобно тому, как по отпечаткам пальцев можно идентифицировать личность, которая эти отпечатки оставила, так и по характеристическим признакам можно определить режимы течения в пласте (рис. 5.2.3).

Все режимы течения можно «опознать» на одном графике.

По этой причине билогарифмический график кривых давления и производной давления называется диагностическим графиком.