Постановка задачи линейного программирования и свойства ее решений

Линейное программирование (ЛП) — раздел математического программирования, применяемый при разработке методов отыскания экстремума линейных функций нескольких переменных при линейных дополнительных ограничениях, налагаемых на переменные. По типу решаемых задач его методы разделяются на универсальные и специальные. С помощью универсальных методов могут решаться любые задачи линейного программирования (ЗЛП). Специальные методы учитывают особенности модели задачи, ее целевой функции и системы ограничений.
Особенностью задач линейного программирования является то, что экстремума целевая функция достигает на границе области допустимых решений. Классические же методы дифференциального исчисления связаны с нахождением экстремумов функции во внутренней точке области допустимых значений. Отсюда — необходимость разработки новых методов.
Общей задачей линейного программирования называют задачу

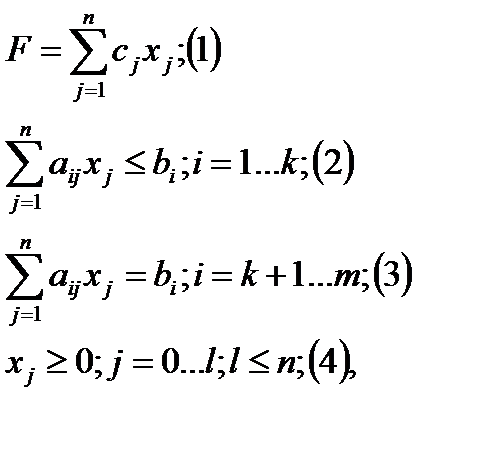
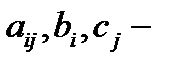
где - заданные действительные числа; (1) – целевая функция (ЦФ); (2) – (4) –ограничения; 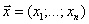- план задачи.

Теорема. Если ЗЛП имеет решение, то целевая функция достигает экстремального значения хотя бы в одной из крайних точек многогранника решений. Если же целевая функция достигает экстремального значения более чем в одной крайней точке, то она достигает того же значения в любой точке, являющейся их выпуклой линейной комбинацией.