Симплекс – метод решения задач линейного
Программирования
Симплекс-метод является универсальным методом, которым можно решить любую задачу линейного программирования с любым числом переменных.
Общая идея симплексного метода (метода последовательного улучшения плана) для решения ЗЛП состоит
1)умение находить начальный опорный план;
2)наличие признака оптимальности опорного плана;
3) умение переходить к нехудшему опорному плану.
Постановка задачи.
Определить максимум целевой функции
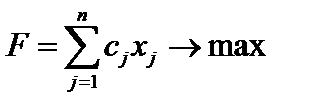 (1)
(1)
при системе ограничений, в которой число уравнений m меньше чем число неизвестных n (m<n).
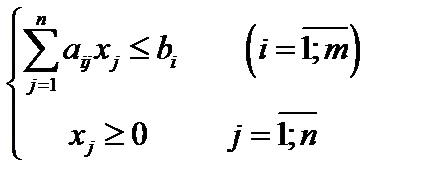 (2)
(2)
Алгоритм симплекс-метода:
1. В системе ограничений (2) свободные члены должны быть со знаком плюс, если встречается отрицательный, то соответствующее неравенство умножается на (-1).
2. Неравенства заменяются уравнениями путем введения добавочных переменных. Получается система из m уравнений с n переменными.
3. m добавочных переменных принимают за основные. выражают основные переменные через неосновные. Находят соответствующее базисное решение, где неосновные переменные равны нулю.
4. Если оно окажется недопустимым, то нужно найти допустимое или установить, что система ограничений противоречива.
5. Выразить целевую функцию через неосновные переменные, полученного допустимого базисного решения. Проверитькритерии оптимальности: если ищется максимум целевой функции и в ее выражении нет неосновных переменных с положительными коэффициентами, то найдено оптимальное решение. Если ищется минимум целевой функции, то в ее выражение не должно быть неосновных переменных с отрицательными коэффициентами).
6. Если оптимальное решение не достигнуто, то находят новое базисное решение. При этом в основные переменные переводят ту неосновную переменную, которая входит с наибольшим по модулю коэффициентом в целевую функцию.
7. Одну из основных переменных переводят в неосновные. Для того, чтобы решить какую именно находят модули отношений свободных членов уравнений к коэффициентам при переменной, которую перевели в основные. При этом, если знаки коэффициентов и свободных членов совпадают или коэффициенты равны нулю, то указанные отношения полагают равными бесконечности. Из этих отношений выбирают наименьшее и соответствующую переменную переводят в неосновные, а соответствующее уравнение выделяют рамкой.
8. Начиная с выделенного уравнения, выражают новые основные переменные и целевую функцию через неосновные переменные.
9. Повторяют пункты (6)-(8) до тех пор, пока не достигнут критерия оптимальности. Затем выписывают переменные, при которых целевая функция оптимальна, и находят ее значение.
Пример.Для выпуска изделий двух четырех видов продукции используется сырье трех типов I, II, III. Расход сырья каждого вида на изготовление единицы продукции заданы таблицей 1. В ней же приведены количества запасов сырья каждого вида и цена реализации одной единицы изделий типа А и типа В.
Таблица 1.
| Сырье Изделия | I | II | III | Прибыль |
| А | ||||
| В | ||||
| С | 2,5 | |||
| D | ||||
| Запасы |
Составить план выпуска продукции, обеспечивающий максимальную прибыль.
Решение.
I этап. Составим экономико-математическую модель задачи.
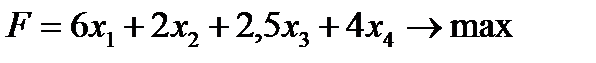 1. Введем переменные: х1- количество изделий первого вида; х2- количество изделий второго вида, х3 – третьего и х4 -четвертого.
1. Введем переменные: х1- количество изделий первого вида; х2- количество изделий второго вида, х3 – третьего и х4 -четвертого.
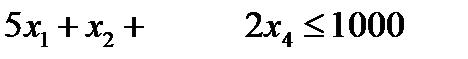
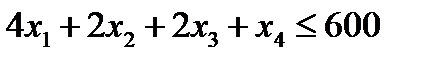
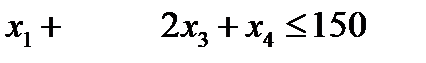
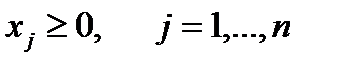
1. Приведем систему ограничений к каноническому виду, то есть заменим неравенства равенствами, для чего введем в каждое неравенство добавочную переменную.
Приведем систему ограничений к каноническому виду, то есть заменим неравенства равенствами, для чего введем в каждое неравенство добавочную переменную.
Найдем первое базисное решение. Для этого за основные переменные выберем добавочные переменные, а за неосновные переменные – первоначальные. Выразим основные переменные через неосновные.
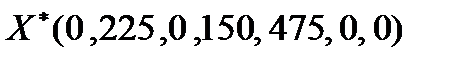
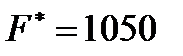 Полученное решение
Полученное решение
можно прочитать следующим образом: для обеспечения максимума прибыли, который составит 1050 денежных единиц, необходимо выпускать 225 единиц продукции второго вида и 150 – четвертого, выпускать продукцию первого и третьего видов не выгодно. При это второй и третий вид сырья расходуется полностью, а первый остается в количестве 150 единиц.
Дата добавления: 2016-01-30; просмотров: 1306;
