Графический способ решения ЗЛП

Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в пространствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практического значения, однако его рассмотрение проясняет свойства ОЗЛП, приводит к идее ее решения, делает геометрически наглядными способы решения и пути их практической реализации.

В соответствии со свойствами решения задач ЛП множество допусти­мых решений задачи ЛП есть выпуклый многогранник n-мерного простран­ства, при чем оптимум ЦФ, если он существует, достигается в одной из вершин этого многогранника (когда оптимальное решение единственно) или на грани много­гранника (если оптимальных решений множество).

На рисунке слайд №12 (Модели линейного программирования 1) приведены примеры выпуклых многоугольников (синим цветом) и невыпуклых (красным цветом). Множеством решений линейного неравенства является одно из полупространств, на которое делится все пространство ги­перплоскостью с уравнением. При наличии лишь двух переменных полупространство превращается в полуплоскость.

Итак, требуется найти графическое решение задачи

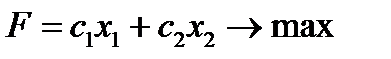
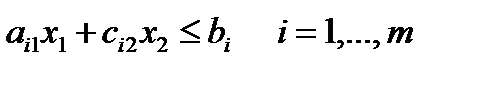
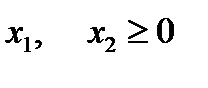
Графическое решения состоит из дух этапов:

1. построение области (многоугольника) допустимых решений ;

2. нахождение оптимума ЦФ .

1. Этап. Построим координатную плоскость с осями х1 и х2. На этой плоскости стоится область допустимых решений системы ограни­ченийзадачи ЛП. Как уже известно, область имеет вид выпуклого много­угольника. ( ограниченного или неограниченного). Для ее построения по очереди решаются неравенства системы ограничений и находится об­ласть, каждая точка которой удовлетворяет всем ограничениям сис­темы.

Для графического решения неравенства

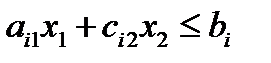
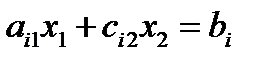строится прямая, которая задается уравнением

Любая прямая определяется двумя точками, н-р одна – пересечение прямой с осью х1, вторая с осью х2. Координаты этих точек имеют след вид

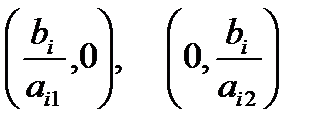
Построенная прямая делит плоскость на две полуплоскости. В одной нера­венство выполняется (ей принадлежит и сама прямая линия), а в другой – нет. Определим область, в которой неравенство (ограничение) выполняется. Для этого выберем произвольную точку на координатной плоскости (например, на­чало координат) и подставим ее координаты в левую часть неравенства. Если неравенство верно, то искомая полуплоскость находится с той же сто­роны от прямой, что и точка, в противном случае искомая полуплоскость ле­жит с противоположной стороны от прямой.

Эти действия выполняются последовательно для всех неравенств.

Пусть система ограничений для нашего случая состоит из 4- нера­венств. Аналогичным образом построим 2-ю прямую.

Допустим, что в 3-м неравенстве содержится лишь одна переменная – х1, в этом случае соответствующее уравнение прямой задает вертикальную линию, которая пересекается с Ох1 в точке с координатами

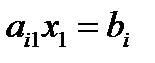
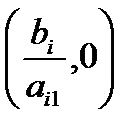
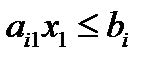
Пусть в четвертом неравенстве присутствует то же лишь одна пере­менная, но теперь уже х2. В этом случае плоскость делится на две полуплос­кости горизонтальной прямой, которая определяется точкой с координатами

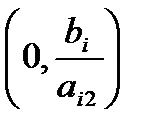
В нашем условно примере 4 ограничения или четыре неравенства, гра­фическое решение которых мы выполнили. Но для построения области до­пустимых решений нужно учесть, что она ограничена осями координат, так как обе переменные величины неотрицательные.

Теперь можно построить область допустимых решений как область пе­ресечения m полуплоскостей, соответствующих m ограничениям задачи. В нашем условном примере m=4. Полученная область имеет вид выпуклого многоугольника. 1 этап кончен - область построена.

2 этап. Этот этап заключается в отыскании такой точки среди точек многоугольника допустимых решений, в которой ЦФ принимает максимальное (*или мини­мальное ) значение.

Согласно свойствам ЗЛП эта точка является угловой точкой или иначе вершиной многоугольника допустимых решений (иногда это множество то­чек, принадлежащих одной из граней многоугольника). Чтобы найти эту точку построим линии уровня

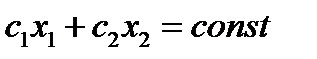
Таких линий можно построит бесконечное множество, т.к. константа = любому положи­тельному числу. . Главная особенность этих линий состоит в том, что ЦФ в любой точке линии принимает одно и то же значение, т.е. меняя значение константы получает множество прямых. Если константа = 0, то эта лини я уровня проходит через начало координат. Для того, чтобы определить направление возрастания ЦФ при переходе с одной линии уровня на другую, построим вектор градиента

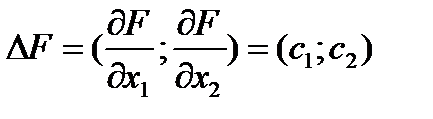
Вектор градиента строится из начала координат в точку с координа­тами (с1, с2). Этот вектор перпендикулярен линиям уровня и он показывает направление возрастания ЦФ. Если решается задача на максимум, то для определения точки оптимума следует двигаться от одной линии уровня к другой в направлении возрастания, пока не произойдет касание с последней точкой многоугольника ДР. Эта точка, как правило, является одной из его вершин или как еще говорят угловых точек. Эта точки и определить максимум ЦФ. Решая задачу на минимум двигаемся навстречу многоугольнику и определяет первую точку, с которой встречается линия уровня. Вычисляем координаты найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка. Эта позволяет определить оптимальные значения х1 и х2. Подставляем полученные значения х в ЦФ и определяем ее максимальное (или минимальное ) значение.

Получаемое решение может быть не единственным, если двигаясь в направлении возрастания или убывания ЦФ линия уровня совпадет на с последней точкой – вершиной многоугольника допустимых решений, с его стороной - в этом случае получаем множество оптимальных значений для х1 и х2.

Особыми случаями является ситуации, когда

1) система ограничений несовместна, невозможно построить многоугольник множества допустимых решений (пример). т.е. это множество пусто;

2) множество допустимых решений сводится к одной точке (пример). В этом случае так же невозможно нахождение оптимального решения.

Итак, алгоритм графического метода решения состоит в следующем:

1. Строится выпуклый многоугольник, соответствующий системе неравенств (2).

2. Строится прямая, линия уровня, соответствующая целевой функции (1) при F = 0, то есть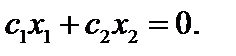

3. Строится вектор 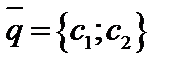перпендикулярный линии уровня с координатами равными коэффициентам целевой функции.

4. При нахождении максимума линия уровня смещается параллельно в направлении вектора 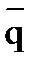, при нахождении минимума – в противоположном направлении.

5. Последняя вершина многоугольника, которую пересечет линия уровня будет экстремумом целевой функции.

6. Вычисляют координаты этой вершины, как координаты точки пересечения соответствующих прямых из системы (2), и подставляя их в целевую функцию, получаем искомое значение.