Электромагнитные затухающие колебания

Электромагнитные затухающие колебания возникают в электромагнитной колебательной систему, называемой LCR – контур (Рисунок 3.3).

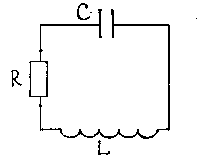
Рисунок 3.3.

Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура: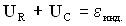

Падение напряжения:

- на активном сопротивлении: 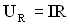, где I – сила тока в контуре;

- на конденсаторе (С): 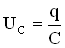, где q – величина заряда на одной из обкладок конденсатора.

ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение: 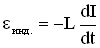(закон Фарадея).

Подставим значения U_R, U_C, 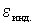в уравнение, отражающее закон Кирхгофа, получим:

.

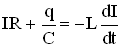Сила тока определяется как производная от заряда 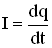, тогда 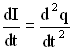, и дифференциальное уравнение примет вид:

.

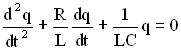Обозначим 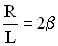, , 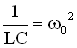получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:

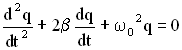
Решение дифференциального уравнения или уравнение колебаний для заряда на обкладках конденсатора имеет вид:

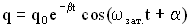или

.

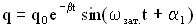Амплитуда затухающих колебаний заряда имеет вид:

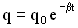, где .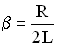

Частота затухающих колебаний в LCR – контуре:

.

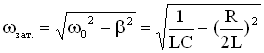Период затухающих электромагнитных колебаний:

.

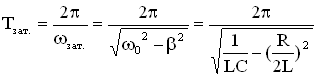Возьмем уравнение для заряда в виде 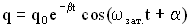, тогда уравнение для напряжения на обкладках конденсатора можно записать так
.

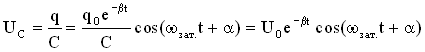Величина 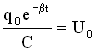называется амплитудой напряжения на конденсаторе.

Токв контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение 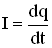и векторную диаграмму.

Окончательное уравнение для силы тока таково:

,

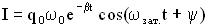где 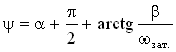- начальная фаза.

Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.

Энергия колебаний в контуре складывается из энергии электрического поля

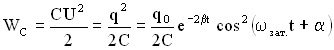
и энергии магнитного поля

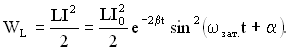
Полная энергия в любой момент времени:

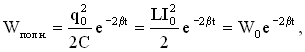
где W₀ – полная энергия контура в момент времени t=0.