Механические затухающие колебания

Механическая система: пружинный маятник с учетом сил трения.

Силы, действующие на маятник:

Упругая сила. 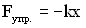, где k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.

Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): 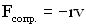. Знак "минус" показывает, что направление силы сопротивления противоположно направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:

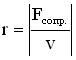
Закон движения пружинного маятника – это второй закон Ньютона:

ma = F_упр. + F_сопр.

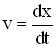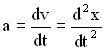Учитывая, что и , запишем второй закон Ньютона в виде:

.

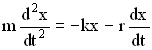Разделив все члены уравнения на m, перенеся их все в правую часть, получим дифференциальное уравнениезатухающих колебаний:

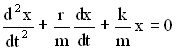
Обозначим 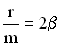, где β – коэффициент затухания, 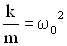, где ω₀ – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе.

В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:

.

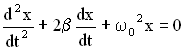Это линейное дифференциальное уравнение второго порядка.

Уравнение затухающих колебаний есть решение такого дифференциального уравнения:

.

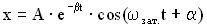
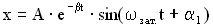В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных.

Частота затухающих колебаний:

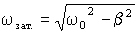(физический смысл имеет только вещественный корень, поэтому ).

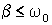Период затухающих колебаний:

.

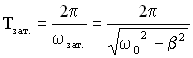Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: .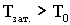

Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении.

Для механической системы пружинного маятника имеем:

, .

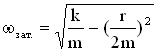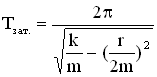Амплитуда затухающих колебаний:

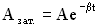, для пружинного маятника .

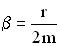Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить.

При небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.

Графики зависимости смещения от времени 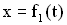и амплитуды от времени 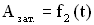представлены на Рисунках 3.1 и 3.2.

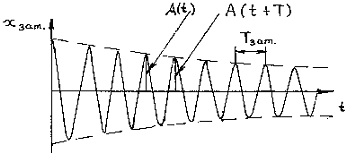
Рисунок 3.1 – Зависимость смещения от времени для затухающих колебаний

Рисунок 3.2 – Зависимости амплитуды от времени для затухающих колебаний