Расчет с использованием ЭВМ.

В настоящее время широкое использование получили методы расчета надежности систем с помощью статических испытаний математической модели аппаратуры на ЭВМ.

При статических испытаниях математической модели аппаратуры на ЭВМ рядом про зондируется некоторая область М, в пределах которой находится точка, отображающая состояние аппаратуры. Точность, с которой определяется положение точки в области 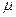, существенно зависит от точности объема исходных данных по элементам, от качества построения мат. модели.

В основе испытаний лежит возможность получения на ЭВМ случайных чисел с различными законами распределения большого количества различных операций с числами по заданному алгоритму.

Основные преимущества:

- моделируются случайные моменты отказа 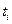, подчиняющиеся любому закону распределения, формируются на ЭВМ последовательности равномерного распределения чисел 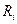в интервале (0,1) и решается уравнение: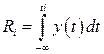

где 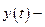плотность распределения вероятности отказов;

- имитируется функционирование схемы на основе моделирования процессов изменения технических параметров, элементов и схем;

- возможность получить дополнительную информацию конструктору о качестве функционирования и общей оценки надежности аппаратуры и отдельных ее устройств;

- автоматизируют вычислительные операции, что упрощает расчет показателей надежности и исключает возможность ошибки при ручном режиме.

Математическая модель РЭА состоит из блок-схемы ее надежности, ряда логических уравнений для независимых отказов, математических правил определения вероятностей отказов, элементов и схем аппаратуры, способов расчета требуемых показателей надежности с заданной точностью и достоверностью. Имитация модели аппаратуры производится с помощью процедуры Монте-Карло, позволяющей учесть случайный характер отказов элементов.

Предполагаются известными аналитические и эмпирические зависимости, связывающие входные характеристики схем (узлов, блоков) с параметрами элементов, а также неравенства, определяющие область, в пределах которой аппаратура сохраняет свою работоспособность. Все данные по элементам, схемам (узлов, блоков) и алгоритм, определяющий порядок действий с этими данными, вводятся в память машины.

Моделирование включает в себя следующие этапы:

- формирование случайных чисел с определенным для каждого элемента законом распределения и его числовыми характеристиками технических параметров;

- определение в данной реализации случайного значения выходного параметра схемы подстановкой в формулу значений технических параметров элементов;

- сравнение случайных значений параметров элементов или моментов их отказов с допустимыми значениями параметров или с заданным временем 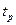безотказной работы и определение на основе этого сравнения состояния аппаратуры;

- повторение предыдущих этапов моделирования 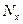раз с целью получения необходимого объема статических данных для расчета с заданной точностью 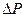и достоверностью у.

Значение вероятности безотказной работы: 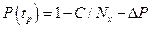, где С- суммарное число отказов, зафиксированное во всех 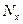реализациях; 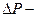требуемая точность.

Сущность моделирования состоит в построении искусственных случайных процессов, определяющих моменты отказов, связанных с параметрами, равными параметрам реальных процессов.

Таким образом, приходится ставить искусственный процесс, что может привести к ошибкам в определении характеристик исследуемых процессов. Наличие ошибок определяется отсутствием достоверных сведений о процессе и ограниченными возможностями ЭВМ.

Необходимость применения методов моделирования диктуется тем, что априорная информация о надежности элемента не дает возможности оценки надежности аппаратуры аналитическим методом.

Оценки показателей надежности, полученные РЭМ, могут быть далеки от истинных, причем величину погрешностей определить не предоставляется возможным.

Оценки надежности, полученные РЭМ, целесообразно применять на стадии проектирования и разработки аппаратуры в качестве ориентировочных для принятия необходимых мер по доработке схем и изменения элементной базы и сравнения по критерию надежности различных вариантов построения систем.