Уравнение свободных незатухающих гармонических колебаний
Колебательный контур – это электрическая цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора емкостью С и резистора сопротивлением R. В идеальном колебательном контуре считается, что сопротивление R пренебрежимо мало (R»0), что позволят в идеальном контуре(рис. 18),состоящем только изкатушки индуктивности и конденсатора, получитьнезатухающие электромагнитные колебания.

Рис. 18
Для возбуждения в контуре колебаний предварительно заряжают конденсатор, сообщая его обкладкам заряд ±q. Тогда в начальный момент времени t=0 (рис. 18, а) между обкладками конденсатора возникнет электрическое поле. Если замкнуть конденсатор на катушку индуктивности, конденсатор начнет разряжаться, и в контуре потечет возрастающий со временем ток I. Когда конденсатор полностью разрядится, энергия электрического поля конденсатора полностью перейдет в энергию магнитного поля катушки (рис. 18, б). Начиная с этого момента ток в контуре будет убывать, и, следовательно, начнет ослабевать магнитное поле катушки, тогда в ней согласно закону Фарадея индуцируется ток, который течет в соответствии с правилом Ленца в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет перезаряжаться, возникнет электрическое поле, стремящееся ослабить ток, который, в конце концов, обратится в нуль, а заряд на обкладках конденсатора достигнет максимума (рис. 18, в). Далее те же процессы начнут протекать в обратном направлении (рис. 18, г), и система к моменту времени t=Т (Т – период колебаний) придет в первоначальное состояние (рис. 18, а). После этого начнется повторение рассмотренного цикла разрядки и зарядки конденсатора, то есть начнутся периодические незатухающие колебания величины заряда q на обкладках конденсатора, напряжения UC на конденсаторе и силы тока I, текущего через катушку индуктивности. Согласно закону Фарадея напряжение UC на конденсаторе определяется скоростью изменения силы тока в катушке индуктивности идеального контура, то есть:
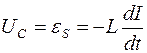 .
.
Исходя из того, что UC=q/C, а I=dq/dt, получаем дифференциальное уравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
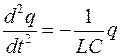 или
или 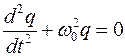 .
.
Решением этого дифференциального уравнения является функция q(t), то естьуравнение свободных незатухающих гармонических колебаний величины заряда q на обкладках конденсатора:
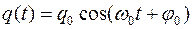 ,
,
где q(t) – величина заряда на обкладках конденсатора в момент времени t;
q0 – амплитуда колебаний заряда на обкладках конденсатора;
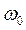 – круговая (или циклическая) частота колебаний (
– круговая (или циклическая) частота колебаний ( 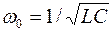 ) ;
) ;
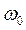 =2
=2 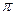 /T (T – период колебаний,
/T (T – период колебаний, 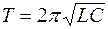 –формула Томсона);
–формула Томсона);
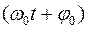 – фаза колебаний в момент времени t;
– фаза колебаний в момент времени t;
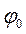 – начальная фаза колебаний, то есть фаза колебаний в момент времени t=0.
– начальная фаза колебаний, то есть фаза колебаний в момент времени t=0.
Дата добавления: 2016-01-29; просмотров: 763;
