Плоскость. Её отображение на чертеже Монжа

Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскость, перпендикулярная хотя бы одной из плоскостей проекций, называется плоскостью частного положения.

Плоскость {∆АВС} является плоскостью общего положения (рис. 20).

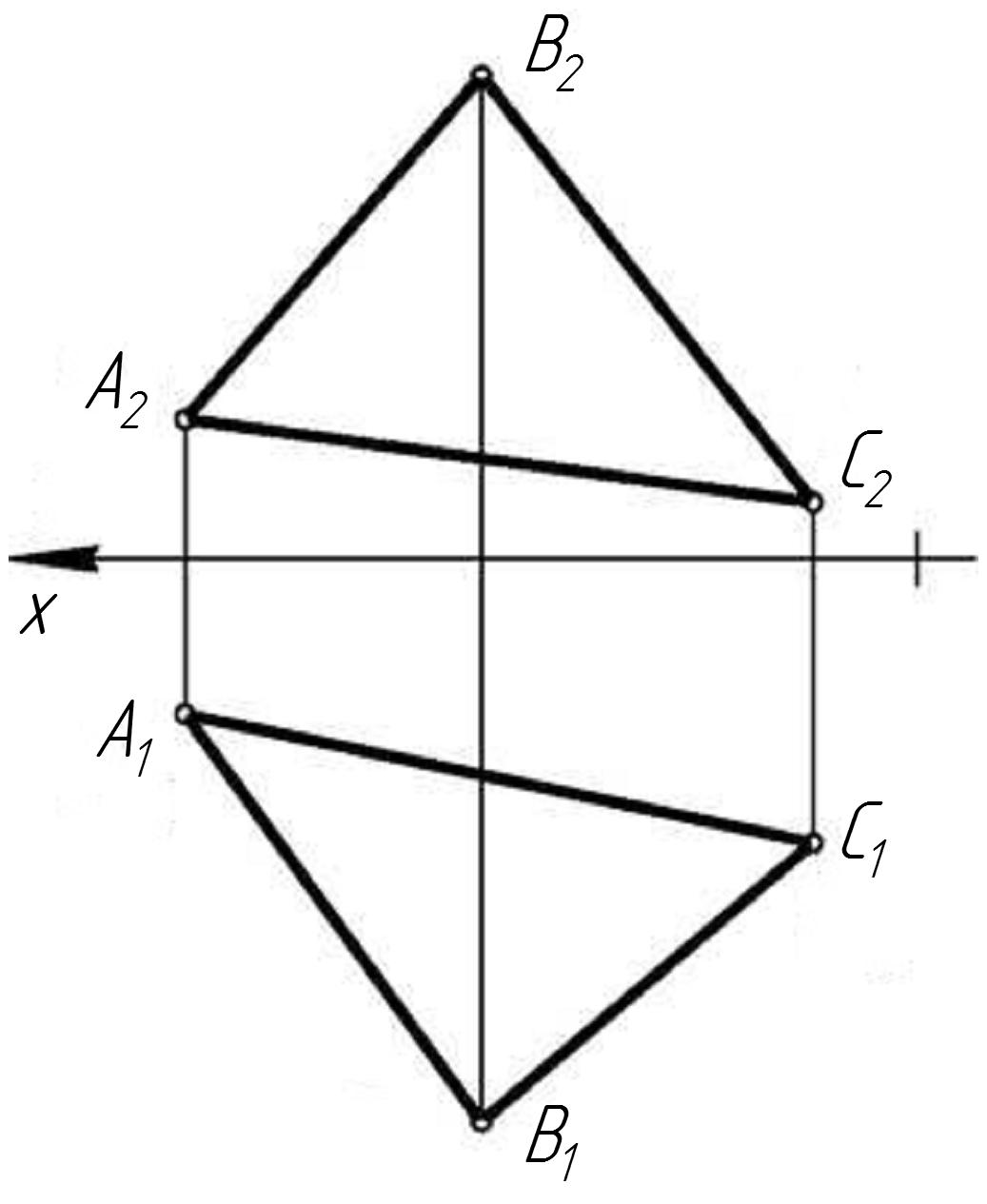
Рассмотрим частные случаи отображения плоскостей. Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня (рис. 21). Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью (рис. 22).

Рис. 20 Плоскость общего положения


P \|\| П₁ - горизонтальная плоскость уровня	Q \|\| П₂ - фронтальная плоскость уровня	R \|\| П₃ - профильная плоскость уровня
Рис. 21 Плоскости уровня

P  П₁ – горизонтально проецирующая плоскость	Q  П₂ – фронтально проецирующая плоскость	R  П₃ – профильно проецирующая плоскость
Рис. 22 Проецирующие плоскости

Взаимное положение прямых

В пространстве две прямые могут совпадать, пересекаться, быть параллельными, скрещиваться.

У совпавших прямых все точки совпадают, поэтому эти прямые будут иметь совпавшие одноименные проекции. По сути, это одна прямая, обозначенная по-разному.

Пересекающиеся прямые имеют одну общую точку. Пусть прямые общего положения а и b пересекаются в точке K (a ∩ b = K). Пересекающиеся прямые, в общем случае, проецируются в пересекающиеся прямые. Точка K – реально существующая точка, и ее проекции находятся на линии проекционной связи (K₁K₂), перпендикулярной оси x (рис. 23).

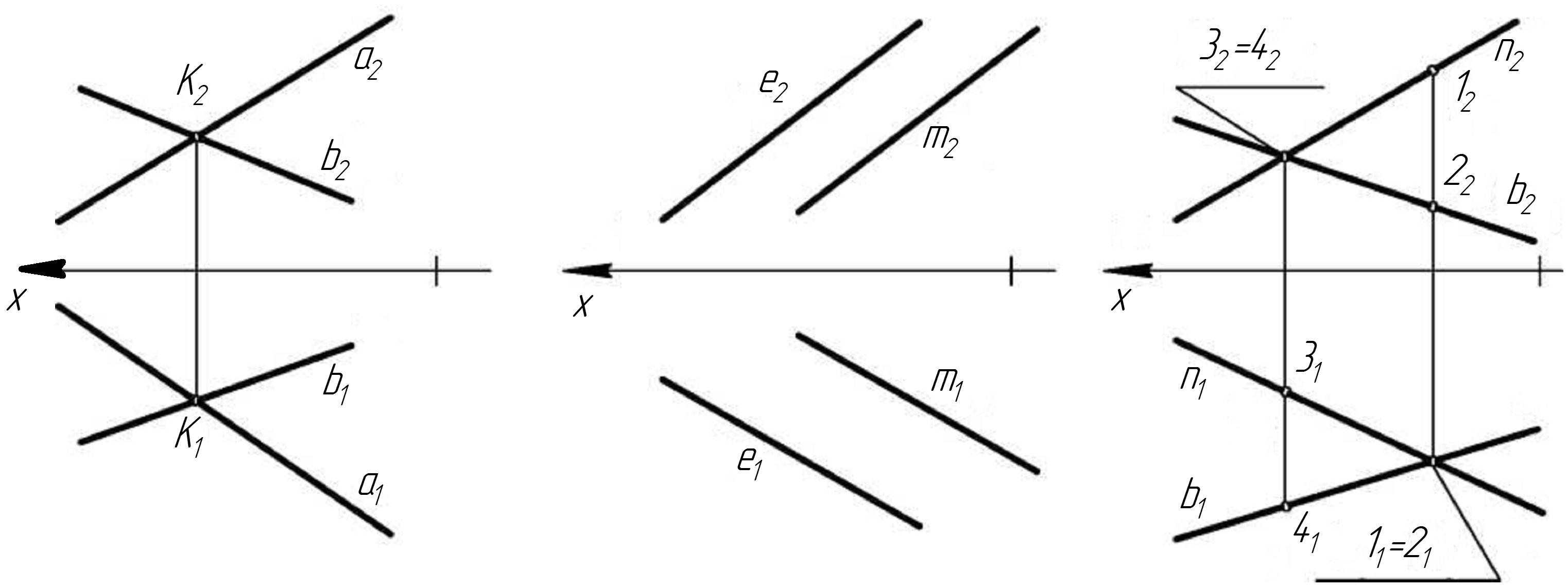
Рис. 23 Пересекающиеся прямые

Рис. 24 Параллельные прямые

Рис. 25 Скрещивающиеся прямые

Параллельные прямые расположены в одной плоскости и не имеют общих точек. Параллельные прямые в общем случае проецируются в параллельные прямые (пятое свойство ортогонального проецирования). На рис. 24 показан комплексный чертеж параллельных прямых e и m. При проецировании этих прямых на П₁ получим е₁ || m₁, при проецировании на П₂ – е₂ || m2.

Прямые, не лежащие в одной плоскости, называются скрещивающимися. Эти прямые не параллельны и не пересекаются. Пример комплексного чертежа скрещивающихся прямых n и b показан на рис. 25 (n ˙ b). Горизонтальные и фронтальные проекции этих прямых пересекаются. Но точки их пересечения не лежат на одной линии проекционной связи. В точке пересечения горизонтальных проекций совпали проекции двух точек 1 Î n и 2 Î b. Это горизонтально конкурирующие точки. Координаты x и у этих точек равны, а координата z точки 1 больше, чем z точки 2. В точке пересечения фронтальных проекций этих прямых совпали проекции двух точек 3 Î n и 4 Î b. Это фронтально конкурирующие точки. Координаты x и z этих точек равны, а координата у точки 4 больше, чем у точки 3. Скрещивающиеся прямые могут проецироваться на одну плоскость проекций в параллельные прямые, а на другую плоскость проекций – в пересекающиеся прямые.

При рассмотрении комплексных чертежей любых фигур необходимо мысленно представлять эти фигуры в пространстве и их положение относительно плоскостей проекций.

<3 4 567 8 9 >

Дата добавления: 2016-01-29; просмотров: 738;