Нанесение надписей и технологических обозначений на чертежах

Наряду с изображениями предмета и размерами чертеж может содержать:

1) текстовую часть, состоящую из технических требований и (или) технических характеристик;

2) надписи с обозначением изображений, а также относящиеся к отдельным элементам изделия;

3) таблицы с размерами и другими параметрами.

Текст, таблицы и надписи располагают параллельно основной надписи чертежа.

Около изображений на полках линий-выносок наносят только краткие надписи, относящиеся непосредственно к изображению предмета. Эти надписи могут содержать не более двух строк, располагаемых над полкой линии-выноски и под ней (рис. 9).

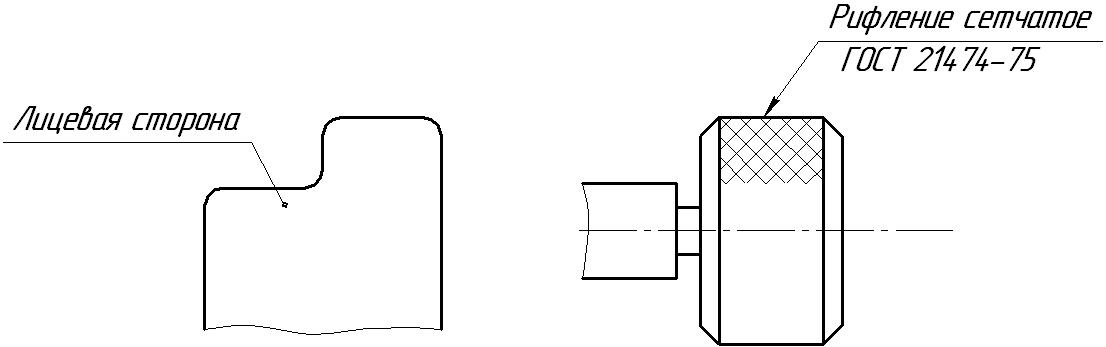
а) б)

Рис. 9 Линии-выноски для надписей около изображений

Линии-выноски не должны пересекаться между собой. На конце линии-выноски, пересекающей контур изображения, ставится точка (рис. 9 а), а линию-выноску, отводимую от линии видимого и невидимого контура, заканчивают стрелкой (рис. 9 б).

Технические требования и техническая характеристика служат для более полного описания характеристик и свойств изделия. Заголовок «Технические требования» не пишут, если на поле чертежа не указывают техническую характеристику изделия. Если на чертеже необходимо указать техническую характеристику, то ее размещают отдельно от технических требований, с самостоятельной нумерацией. В таком случае над техническими требованиями помещают заголовок «Технические требования», а над технической характеристикой – «Техническая характеристика».

ОРТОГОНАЛЬНОЕ (ПРЯМОУГОЛЬНОЕ) ПРОЕЦИРОВАНИЕ

И ЕГО СВОЙСТВА

Изображение пространственных тел на плоскости основано на методе проецирования.

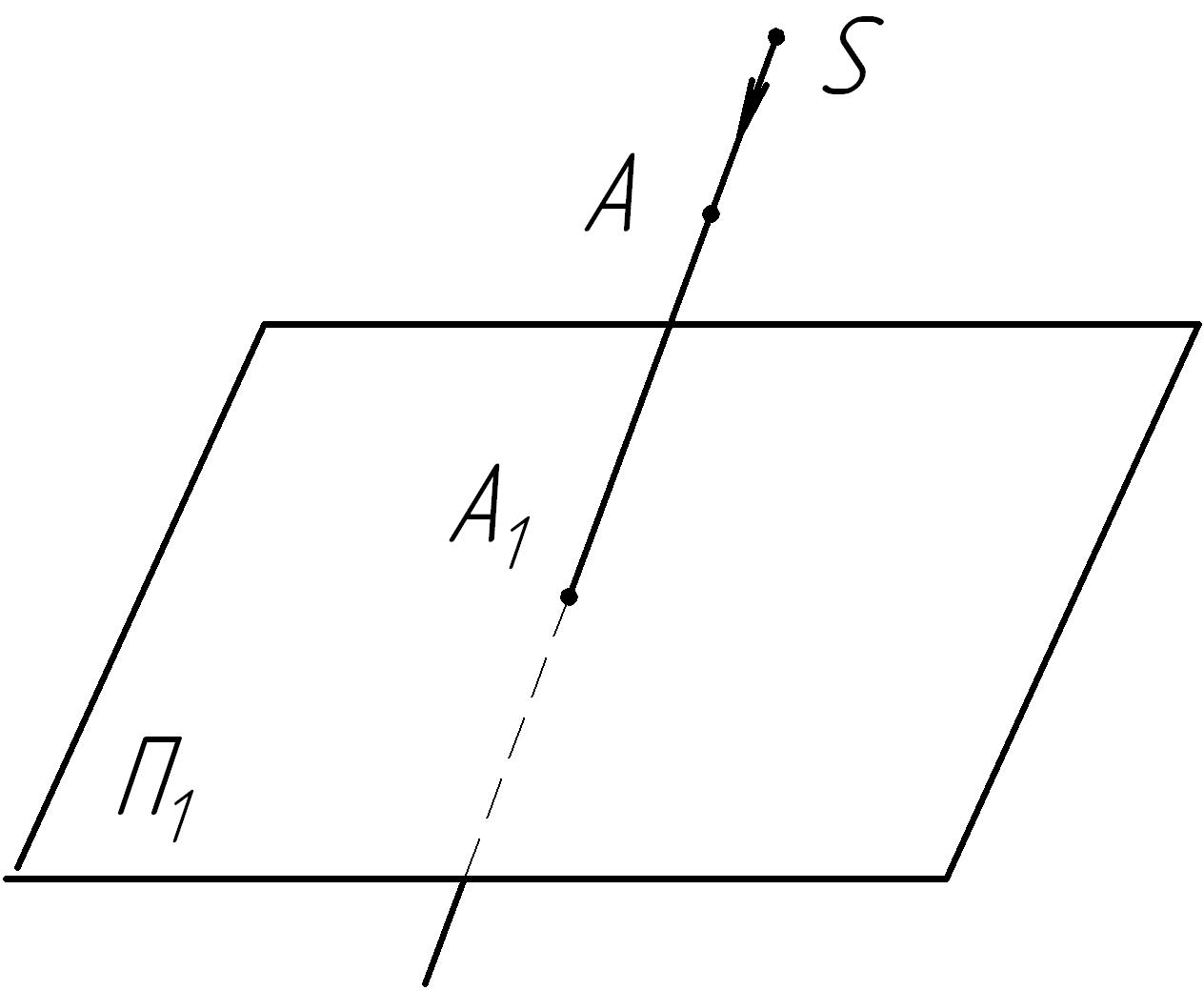
Представим некоторую заданную плоскость П₁ и точку А в пространстве (рис. 11). Луч, проведенный из точки S через точку А в направлении плоскости П₁, пересечет ее в некоторой точке А₁. Точку А называют проецируемой точкой, плоскость П₁, на которой получают проекцию, называют плоскостью проекций. Точка пересечения луча с плоскостью называется проекцией точки А. Луч, при помощи которого находится проекция точки, называется проецирующим лучом.

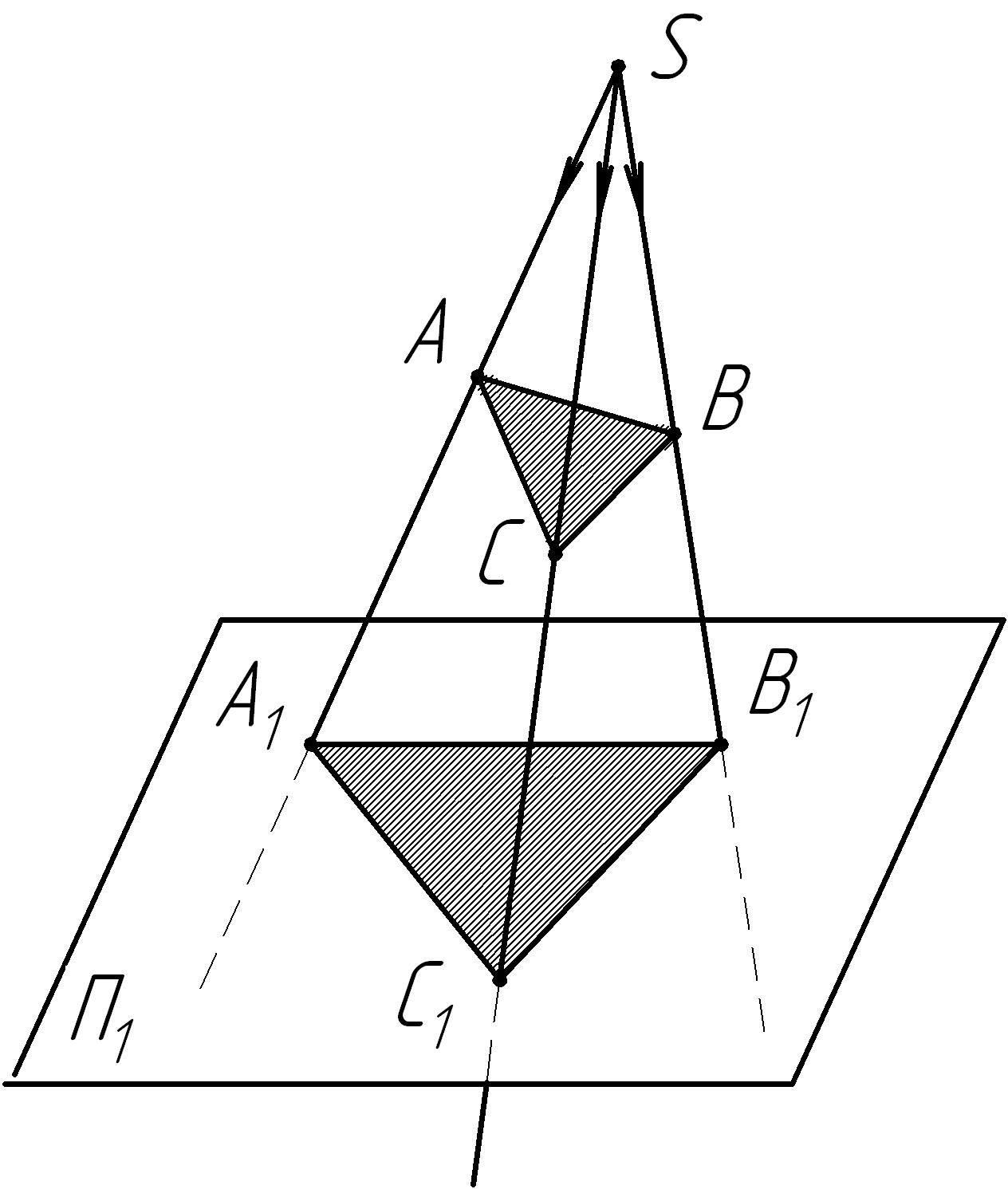
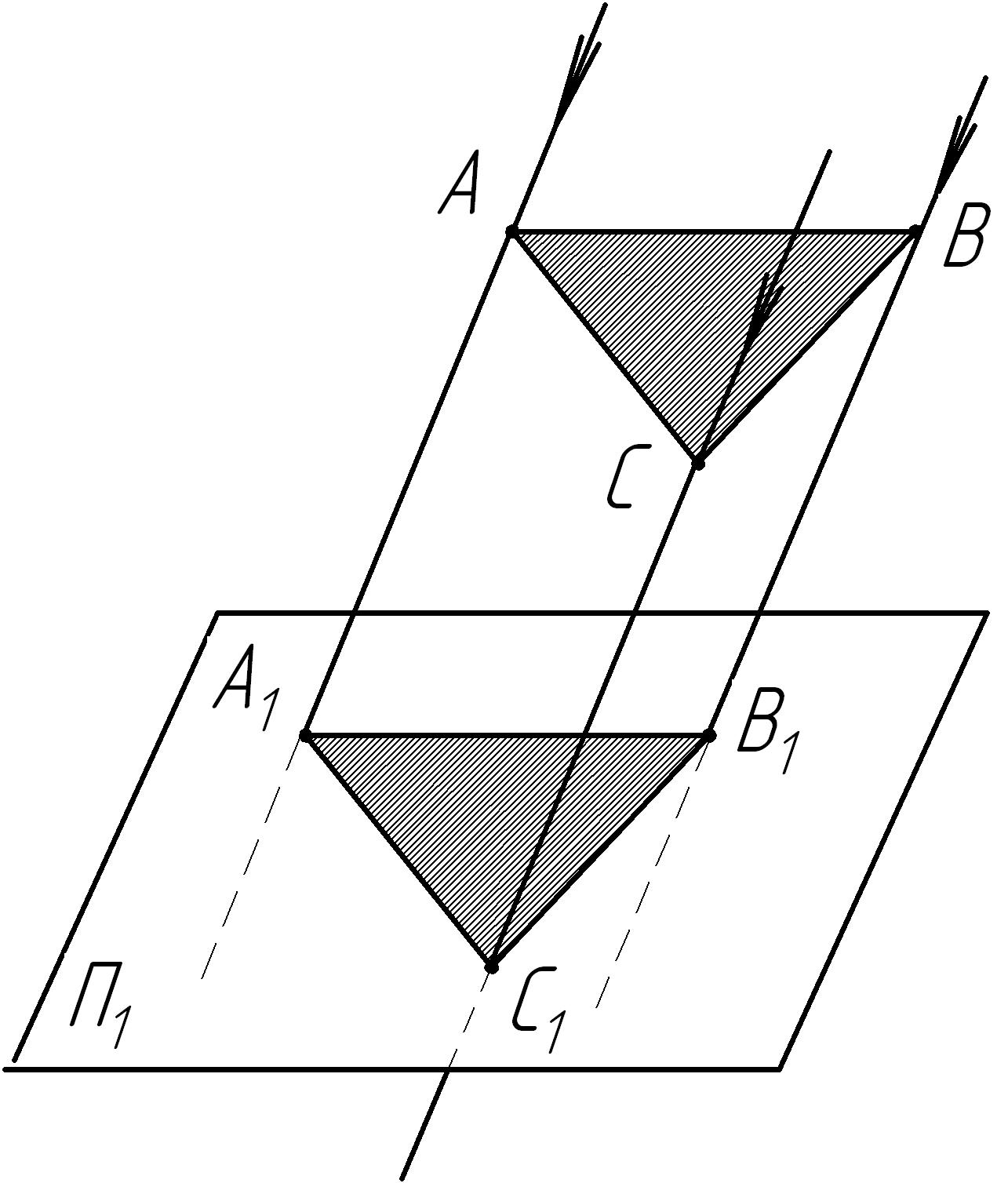
Рис. 12 Центральная проекция плоского треугольника

Рис. 13 Параллельная проекция плоского треугольника

Проекция предмета, построенная методом центрального проецирования, называется перспективой.

При параллельном проецировании используют «пучок» параллельных проецирующих лучей, проходящих через все точки проецируемого предмета (рис. 13).

В зависимости от угла наклона проецирующих лучей к плоскости проекций параллельное проецирование бывает прямоугольным – когда проецирующие лучи перпендикулярны плоскости проекций, и косоугольным – проецирующие лучи не перпендикулярны к плоскости проекций. Прямоугольные проекции называют также ортогональными.

Рассмотрим основные свойства ортогонального проецирования.

1. Точка проецируется в точку (проекцией точки является точка).

2. Прямая, в общем случае, проецируется в прямую. Прямая, перпендикулярная плоскости проекций, проецируется в точку.

3. Если точка принадлежит прямой, то ее проекция принадлежит проекции прямой.

4. Пересекающиеся прямые в общем случае проецируются в пересекающиеся прямые. Это легко доказать, если для точки пересечения прямых применить свойство 3.

5. Параллельные прямые в общем случае проецируются в параллельные прямые.

6. Отрезок проецируется в отрезок. Отрезок, перпендикулярный плоскости проекций, проецируется в точку. Длина проекции отрезка равна длине отрезка, умноженной на косинус угла наклона отрезка к плоскости проекций (при проецировании на П₁: |A₁B₁| = | AB| cos α).

Отрезок параллельный плоскости проекций проецируется на нее в параллельный и равный себе отрезок.

7. Отношение длин отрезков AB и CD, лежащих на параллельных прямых или на одной прямой, при проецировании не меняется.

8. Фигура, принадлежащая плоскости параллельной плоскости проекций, проецируется на плоскость проекций в равную ей фигуру (в натуральную величину).

9. Если две плоскости проекций параллельны, то проекции любой фигуры на эти плоскости равны.