Экономических процессов

Сложность и динамичность, а также высокий уровень неопределенности, являясь характерными свойствами экономических процессов, порождают специфические условия, которые необходимо учитывать при разработке прогнозных моделей. Эта специфичность должна быть определяющей как при выборе адаптивных моделей и алгоритмов для проведения конкретных прогнозных расчетов, так и в работе по дальнейшему совершенствованию подходов, основанных на применении принципов адаптации в экономических исследованиях. Поэтому среди большого разнообразия методов адаптивного управления и предсказания широкое распространение в экономических приложениях получили только те, которые в наибольшей мере удается приспособить к требованиям этой специфики.

В настоящее время наибольшей популярностью у специалистов пользуются модели, адаптивный механизм которых построен на основе использования процедуры экспоненциального сглаживания. Модели с подобным механизмом находят применение как при решении прикладных задач, так и в теоретических построениях. И дело здесь не только и не столько в простоте идеи и удобстве вычислительной схемы, хотя и это играет определенную роль. Скорее, успех объясняется тем, что с ее помощью удается построить эффективный механизм корректировки коэффициентов прогнозной модели в ситуациях, когда специфичность условий экономического развития проявляется отсутствием информации, по которой можно было бы определить закономерность, лежащую в основе структурных изменений модели. Конечно, с подобной ситуацией приходится сталкиваться и в технических приложениях, но все же характерной, а практика решения задач перспективного анализа не оставляет места сомнениям по этому поводу, она является для приложений экономического плана.

Отсутствие информации может быть компенсировано только использованием правдоподобных предположений о характере поведения модели в ответ на качественные изменения в развитии моделируемых процессов. Пожалуй, самой простой и вполне естественной для экономических процессов является гипотеза, в основу которой положено предположение о том, что в моделях, отражающих эти закономерности, с течением времени происходит сравнительно медленное изменение структурных коэффициентов. Фактически это предположение непосредственно вытекает из анализа результатов одновременного проявления динамичности и инерционности экономических систем, так как именно одновременное действие ограничивает яркое проявление только одного из этих свойств, исключая тем самым применение как моделей с постоянными коэффициентами, так и моделей с резко изменяющимися свойствами. Удобным инструментом для практической реализации этой гипотезы как раз и явился метод экспоненциального сглаживания.

Применение метода экспоненциального сглаживания в краткосрочном прогнозировании получило широкое распространение после выхода работ П. Винтерса, Р. Брауна, Р. Майера, в которых дано его обоснование для случая моделей полиномиального типа. Учитывая этот факт в истории развития методов адаптивного прогнозирования экономических процессов, рассмотрим основные принципы их построения на примере модели, представляющей собой полином нулевого порядка

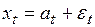, (5.1)

где 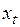– значение показателя, характеризующего уровень прогнозируемого процесса в момент времени ;

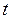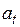– изменяющийся во времени параметр, характеризующий средний уровень прогнозируемого процесса в момент времени ;

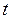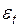– случайные независимые отклонения фактических значений от текущего среднего, имеющие нулевое математическое ожидание и конечную дисперсию .

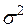Согласно этой модели расчетная величина прогнозного значения 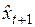полагается равной оценке параметра 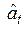, т.е.

. (5.2)

В свою очередь, за оценку текущего значения параметра 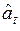принимается экспоненциальная средняя 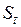, рассчитываемая по рекуррентной формуле

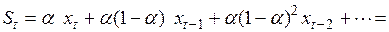
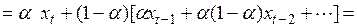
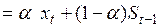(5.3)

где 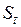– значение экспоненциальной средней в момент ;

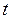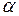– параметр сглаживания, .

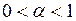Фактически схема расчета прогнозной величины задается рекуррентной формулой (5.3), в которой при определении текущей средней используется механизм старения данных по экспоненциальному закону, позволяющий построить прогнозную траекторию с преобладанием тенденций последнего периода. Причем степень этого преобладания может регулироваться параметром 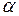. Чем ближе 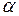к 1, тем меньше прогнозная оценка отличается от последнего наблюдения.

Для экономических процессов такой механизм хорошо согласуется с интуитивным представлением о характере взаимосвязи будущего их состояния с достигнутыми уровнями предшествующих периодов и, по сути, является адаптивным. Чтобы выяснить сущность принципов, положенных в основу адаптивного механизма рассматриваемой модели, перепишем (5.3) в виде

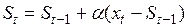. (5.4)

Если теперь 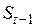рассматривать как величину прогнозного значения для момента 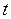, то в выражении (6.4) разность 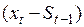представляет собой погрешность прогноза. Эта погрешность учитывается в качестве корректирующего слагаемого при расчете нового прогнозного значения 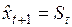. Таким образом, в вычислительной схеме экспоненциального среднего используется принцип регулятора с обратной связью, что позволяет говорить об адаптивных свойствах модели (5.1).

Таким образом, экспоненциальное сглаживание лежит у истоков адаптивных методов, а сущность этих методов прогнозирования можно раскрыть следующим образом: «Адаптивными называются методы прогнозирования, позволяющие строить самокорректирующиеся (самонастраивающиеся) экономико-математические модели, способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда»[1].