Оценка точности прогнозных расчетов по моделям ARIMA

Как известно, основное предназначение моделей ARIMA– прогнозные расчеты. При выполнении этих расчетов возникает естественный вопрос об оценке точности получаемых прогнозных значений. Ошибки в прогнозных расчетах неизбежны. По крайней мере, есть два источника, порождающих эти ошибки. Первый – невозможность предугадать уровень случайной составляющей 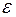в будущих значениях прогнозируемого показателя, второй – отклонение оценок коэффициентов авторегрессионной модели, полученных с помощью МНК, от их истинных значений. Рассмотрим ситуацию, когда оценивается точность прогнозных расчетов в рамках теоретической модели процесса ARIMA(1,0,1)

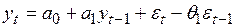(4.59)

в зависимости от первого источника.

Прогнозная оценка для периода 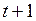может быть представлена в виде

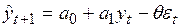, (4.60)

а ее ошибка получается путем вычитания (4.60) из (4.59)

. (4.61)

Таким образом, дисперсия прогноза на один шаг вперед равна дисперсии случайной составляющей

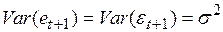. (4.62)

Прогнозная оценка для периода 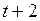представима в виде

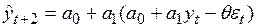. (4.63)

Вычтя прогнозную оценку из уравнения

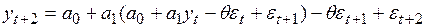, (4.64)

получаем ошибку прогноза

, (4.65)

дисперсия которой равна

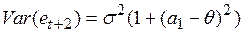. (4.66)

Последовательно продолжая рекуррентное вычисление прогнозных оценок, можно получить выражение

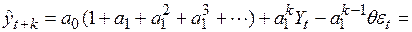
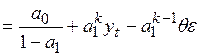, (4.67)

из которого следует, что в случае стационарности ( 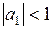) и обратимости ( 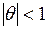) процесса прогноз стремится к среднему 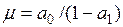. Этот факт позволяет сделать вывод, что дисперсия прогнозной ошибки

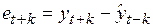(4.68)

в пределе при 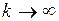стремится к дисперсииARMA (1,1), так как

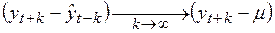(4.69)

и дисперсия предельной ошибки ни что иное, как известная нам дисперсия процесса ARMA (1,1)

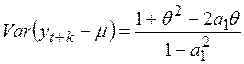. (4.70)