Графический расчет кинематики
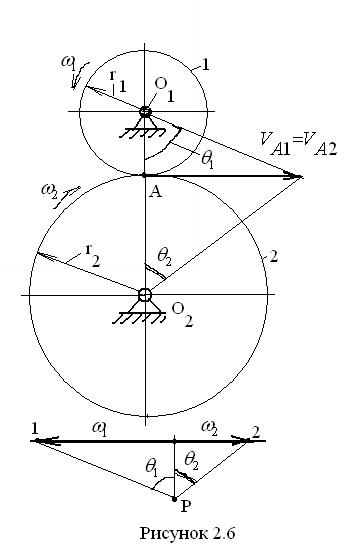Методика графического расчёта основана на том, что окружные скорости центроидных окружностей колес одинаковы, а в точке касания этих окружностей их направления совпадают. Зубчатые колёса, показанные на рисунке 2.6, вращаются навстречу друг другу так, что в точке А касания их центроидных окружностей окружные скорости совпадающих точек А1 и А2 также совпадают. Имея в виду, что скорость точки, совершающей вращательное движение вокруг неподвижной точки, линейно зависит от её расстояния от последней, то есть
V =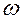 
· r ,
заключаем, что концы векторов скоростей точек, лежащих на прямой О1О2, принадлежащих колесу 1, лежат на одной прямой, называемой линией распределения скоростей этого колеса. То же самое имеет место и с точками колеса 2, лежащими на линии центров колёс.
Проведём горизонтальную прямую ниже изображения колёс и на некотором расстоянии от этой прямой возьмём произвольную точку P. Из неё проведём прямые параллельно линиям распределения скоростей до пересечения с горизонталью в точках 1 и 2. Запишем цепочку равенств, имея в виду предыдущие рассуждения и подобие треугольников на картине зацепления и на нижнем построении:
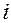12 = 
.
Учитывая начало этого равенства и его конец, можно сделать вывод, что отрезки, полученные на горизонтали, в некотором масштабе изображают угловые скорости колёс. Для определения масштаба угловых скоростей необходимо угловую скорость 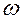1 (если, конечно, она задана) поделить на отрезок 
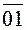, измеренный в миллиметрах. Угловая скорость 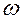2 определится умножением этого масштаба на отрезок 
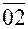, взятый также в миллиметрах. На основе изложенной методики можно достаточно просто решить задачу кинематики любого зубчатого механизма. Если требуется определить передаточное отношение механизма, то достаточно взять отношение отрезков, выражающих соответствующие угловые скорости.
З а м е ч а н и е . В дифференциальных механизмах с замкнутым контуром (схема В рис. 2.5), как правило, ведущим звеном является центральное колесо дифференциальной ступени, и построение картины линейных скоростей от этого колеса невозможно. Для решения задачи необходимо выбрать в качестве ведущего любое другое звено и задаться произвольно его окружной скоростью. После этого задача решается без затруднений.
Вопросы для самопроверки
1. Для чего применяются зубчатые механизмы?
2. Что такое передаточное отношение?
3. Какие зубчатые механизмы называют редукторами, мультипликаторами?
4. Как можно выразить передаточное отношение в паре зубчатых колёс?
5. Изобразите схему рядового, ступенчатого соединений зубчатых колёс.
5. Какая связь между передаточным отношением сложного зубчатого механизма и передаточными отношениями отдельных его ступеней?
6. Как определяется передаточное отношение в механизмах с рядовым и ступенчатым соединениями колёс?
7. Какие зубчатые механизмы являются механизмами планетарного типа (эпициклическими)?
8. В чём состоит основное достоинство механизмов планетарного типа?
9. Назовите элементы типовой схемы механизма планетарного типа.
10. Для чего и как применяется метод обращения движения?
11. Каковы особенности аналитического расчета механизмов планетарного типа различных схем?
12. На чём основан графический метод исследования кинематики зубчатых механизмов?
13. Какова особенность графического расчёта кинематики дифференциального механизма с замкнутым контуром?
Дата добавления: 2016-01-29; просмотров: 827;