Механизм с рядовым соединением колес
В этом механизме все колеса вращаются в одной плоскости, и каждое промежуточное колесо образует зацепление с двумя соседними (рис. 2.2).
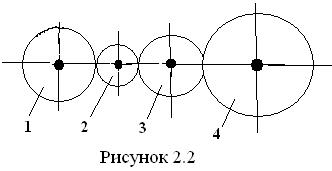 На схеме механизма цифрами обозначены номера колёс, а неподвижные оси затушёваны.
На схеме механизма цифрами обозначены номера колёс, а неподвижные оси затушёваны.
Согласно доказанному выше положению общее передаточное отношение данного механизма определяется равенством:
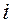 14 =
14 = 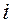 12 ·
12 · 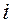 23·
23· 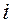 34.
34.
Записав передаточные отношения отдельных ступеней
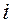 12 = –
12 = –  2/
2/  1,
1, 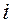 23 = –
23 = –  3/
3/  2 и
2 и 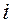 34 = –
34 = –  4/
4/  3
3
и подставив их в правую часть полученного ранее произведения, имеем
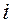 14 = (–
14 = (–  2/
2/  1)·(–
1)·(–  3/
3/  2)·(–
2)·(–  4/
4/  3),
3),
что после выполнения необходимых действий приводит к следующему результату
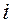 14 = –
14 = –  4/
4/  1.
1.
Этот результат показывает, что в механизмах такого типа передаточное отношение зависит только от чисел зубьев ведущего и ведомого колёс. Промежуточные колёса, числа зубьев которых не влияют на передаточное отношение, называются паразитными. Они позволяют только передать движение на небольшое расстояние и изменить его знак. Для общего случая механизма с произвольным числом колёс при вычислении передаточного отношения можно руководствоваться следующим выражением 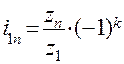 ,
,
где k – число внешних зацеплений, т. к. только они влияют на знак результата.
Механизм со ступенчатым соединением колёс
В этом механизме колеса вращаются в параллельных плоскостях, и каждое промежуточное колесо вступает в зацепление с одним соседним колесом. На каждом промежуточном валу имеется по два колеса. На рисунке 2.3 показана схема
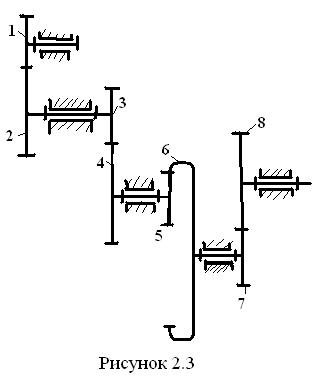 механизма, в котором на промежуточных валах вращаются колёса 2 и 3, 4 и 5, 6 и 7, на ведущем валу находится одно колесо 1, а на ведомом – также одно колесо 8. Найдём передаточное отношение от первого колеса к восьмому
механизма, в котором на промежуточных валах вращаются колёса 2 и 3, 4 и 5, 6 и 7, на ведущем валу находится одно колесо 1, а на ведомом – также одно колесо 8. Найдём передаточное отношение от первого колеса к восьмому 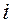 18. Для этого сначала запишем
18. Для этого сначала запишем
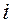 18 =
18 = 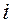 12 ·
12 · 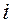 34 ·
34 · 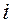 56 ·
56 · 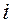 78.
78.
Так как 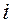 12 = –
12 = –  2/
2/  1,
1, 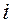 34 = –
34 = –  4/
4/  3,
3, 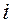 56 =
56 =  6/
6/  5 и
5 и 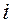 78 = –
78 = –  8/
8/  7, то, подставив в произведение передаточных отношений эти дроби, получим окончательно
7, то, подставив в произведение передаточных отношений эти дроби, получим окончательно
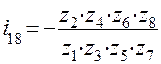 .
.
Никаких сокращений здесь нет кроме возможных общих множителей после подстановки чисел зубьев. Общий знак минус появился из-за того, что в механизме нечётное число пар внешнего зацепления (три пары). По сравнению с предыдущей схемой здесь можно получить практически любое передаточное отношение. Для общего случая механизма запишем формулу передаточного отношения в следующем виде
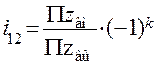 ,
,
где k – число пар колёс внешнего зацепления, а символы в числителе означают произведение чисел зубьев ведомых колёс каждой пары, в знаменателе – произведение чисел зубьев ведущих колёс каждой пары.
Такие механизмы более выгодны с точки зрения преобразования движения, чем механизмы с рядовым соединением колес, т.к. они позволяют получить любое передаточное отношение.
Кинематика механизмов планетарного типа
В отличие от рассмотренных схем существуют механизмы, у которых оси отдельных колес подвижны. Такие механизмы относятся к механизмам планетарного типа или эпициклическим. Эти механизмы по передаточному отношению выгодно отличаются от предыдущих, т. к. они могут обеспечить большое передаточное отношение при малом количестве колес (до 10 тысяч и более при четырех колесах).
Дата добавления: 2016-01-29; просмотров: 1174;
