Характеристики нагрузки на участке ЦСИО.
Как отмечалось выше, в ЦСИО по одним и тем же каналам связи передаются речевые потоки, потоки данных, изображения и др. При этом отдельные виды информации требуют скорости передачи, которую не обеспечивает стандартный цифровой канал с пропускной способностью 64 кбит/с. В такой ситуации на станциях и узлах У-ЦСИО реализуется режим многоканальной коммутации, когда в зависимости от категории вызова производится одновременное занятие нескольких стандартных цифровых каналов.
Как следствие, при математическом описании мультисервисных систем необходимо иметь в виду, что поток вызовов будет отличаться по своим свойствам от потока занятия каналов. В частности, даже при ординарном потоке поступающих вызовов поток занятия каналов будет неординарным, так как для обслуживания отдельных вызовов каналы занимаются группами. С учетом указанного обстоятельства следует различать два понятия нагрузки: нагрузка по вызовам и нагрузка на каналы.
Для некоторого пучка каналов мгновенная интенсивность обслуживаемой нагрузки по вызовам в момент времени t имеет значение j(t), равное числу одновременно обслуживаемых вызовов. В отличие от этого, интенсивность обслуживаемой нагрузки на каналы есть число j(t) одновременно занятых каналов в момент t. В общем случае i(t) ≠ j(t), так как один вызов может занимать сразу несколько каналов.
Из аналогичных соображений в мультисервисных системах с многоканальной коммутацией необходимо различать соответствующие виды поступающей нагрузки: по вызовам и на каналы. В частности, мгновенное значение интенсивности поступающей нагрузки по вызовам в момент времени t есть случайная величина, равная количеству вызовов, которые обслуживаются в рассматриваемый момент воображаемым пучком с бесконечным числом каналов.
Рассмотрим частный случай, когда для обслуживания каждого поступившего вызова требуется одинаковое число т свободных каналов. Тогда в любой момент времени обслуживаемая нагрузка на каналы будет в т раз больше обслуживаемой нагрузки по вызовам: i(t) = m·j(t). Если поток вызовов простейший и характеризуется параметром λ, то поступающая нагрузка по вызовам будет пуассоновской, а ее математическое ожидание Yв и дисперсию DB можно вычислить с помощью следующего соотношения:
YB = DB = λ · h,
где h - среднее время обслуживания одного вызова.
В воображаемом бесконечном пучке каналов, как и в реальном пучке, число занятых каналов будет в т раз больше числа обслуживаемых вызовов. Отсюда вытекают выражения, позволяющие определить интенсивность поступающей нагрузки на каналы и ее дисперсию:
Yk=m·YB = m·λ·h, Dk = m2·DB = m2·λ·h. (12.2)
Здесь применяется следующее правило, известное из теории вероятностей: если случайная величина умножается на постоянный коэффициент, то на этот же коэффициент нужно умножить ее математическое ожидание, а дисперсия должна умножаться на коэффициент в квадрате.
Из приведенных формул видно, что Dk > Yk,и рассматриваемая нагрузка является скученной, что обусловлено неординарностью потока занятий каналов. При этом коэффициент скученности zk равен числу каналов, которые требуются для обслуживания одного вызова,
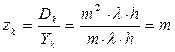 (12.3)
(12.3)
При поступлении вызовов от источников разных категорий формулы (17.7) будут справедливы для математического ожидания и дисперсии нагрузки на каналы, которая создается вызовами i-й категории, i = 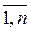 :
:
Yi = mi λi hi,
Di = 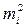 λi hi.
λi hi.
Подставляя эти соотношения в формулу (12.1), можем найти коэффициент скученности объединенной нагрузки на каналы:
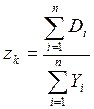 =
= 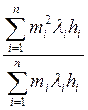 (12.4)
(12.4)
Полученное выражение имеет следующий физический смысл: коэффициент скученности мультисервисной нагрузки равен средневзвешенному числу каналов 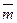 , которые требуются для обслуживания вызовов отдельных категорий, с весами miλihi, равными интенсивности нагрузки на каналы, создаваемой вызовами этих категорий, i =
, которые требуются для обслуживания вызовов отдельных категорий, с весами miλihi, равными интенсивности нагрузки на каналы, создаваемой вызовами этих категорий, i = 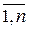 .
.
Дата добавления: 2016-01-29; просмотров: 948;
