Скученность нагрузки.

Если поступающий поток вызовов является простейшим, то создаваемая им нагрузка, как случайная величина, имеет распределение Пуассона. Для случайной величины, которая описывается этим распределением, характерно равенство первых двух моментов, т.е. дисперсия нагрузки совпадает с ее математическим ожиданием. Такая нагрузка называется пуассоновской нагрузкой первого рода и считается равномерной.

Если дисперсия нагрузки меньше ее математического ожидания, то нагрузку называют сглаженной, поскольку ее отклонения от сред­него значения будут меньше, чем для пуассоновской нагрузки.

Нагрузка, у которой дисперсия больше математического ожидания, получила название скученной. В этом случае вызовы поступают неравномерно: для некоторых интервалов времени число поступивших вызовов мало, а на других интервалах число вызовов достигает зна­чительной величины, т.е. вызовы группируются в коротких интервалах времени. К примеру, скученная нагрузка создается так называемым избыточным потоком вызовов, которые потеряны на пучке А и посту­пают для обслуживания на другой пучок В. Этот поток является пре­рывистым, так как на пучок В вызовы могут поступать только при ус­ловии, что в пучке А отсутствуют свободные соединительные устрой­ства.

Скученность z нагрузки измеряется отношением дисперсии нагруз­ки D к ее математическому ожиданию Y:

z =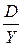

Величина z, которая также называется коэффициентом скученно­сти нагрузки, равна единице для равномерной (пуассоновской) на­грузки, меньше единицы для выровненной (сглаженной) нагрузки и больше единицы для скученной (избыточной) нагрузки.

Если на пучок соединительных устройств поступают сразу не­сколько п потоков вызовов, то математические ожидания Y_i этих на­грузок суммируются. Для статистически независимых потоков также суммируются и дисперсии D_i соответствующих нагрузок. Таким обра­зом, математическое ожидание Y и дисперсия D суммарной нагрузки рассчитываются по следующим формулам:

,

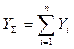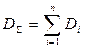
Коэффициент скученности объединенной нагрузки определяется следующим выражением:

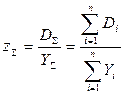. (12.1)