Лекция. Понятие о самоподобном (фрактальном) трафике

Цель лекции: ознакомить с понятием самоподобного трафика, коэффициентом Хёрста, критерием самоподобности.

Содержание:

а) самоподобность трафика сетей с пакетной передачей данных;

б) понятие фрактала и самоподобия;

в) параметр Хёрста.

При проектировании, запуске и эксплуатации телекоммуникационных сетей одной из основных проблем является задача обеспечения качества обслуживания. До недавнего времени решение данной задачи при проектировании систем распределения информации обеспечивала теория телетрафика, которая является одной из ветвей теории массового обслуживания, и появилась в результате работ А.К. Эрланга, Т. Энгсета, Г. О.Делла, К. Пальма, А.Я. Хинчина и др.

Данная теория хорошо описывает процессы, происходящие в таких системах распределения информации, как телефонные сети, построенных по принципу коммутации каналов. Наиболее распространенной моделью потока вызовов (данных) в теории телетрафика является простейший поток (стационарный, ординарный поток без последействия). Настоящий период бурного развития высоких технологий привел к появлению и повсеместному распространению сетей с пакетной передачей данных, которые постепенно стали вытеснять системы с коммутацией каналов, но, по-прежнему, они проектировались на основе общих положений теории телетрафика.

Однако, в 1993 году группа американских исследователей W.Leland,

M.Taqqu, W.Willinger и D.Wilson опубликовали результаты своей новой работы, которая в корне изменила существующие представления о процессах, происходящих в телекоммуникационных сетях с коммутацией пакетов. Эти исследователи изучили трафик в информационной сети корпорации Bellcore и обнаружили, что потоки в ней нельзя аппроксимировать простейшими и, как следствие, они уже имеют совершенно иную структуру, чем принято в классической теории телетрафика. В частности, было установлено, что трафик такой сети обладает так называемым свойством самоподобия., т.е. выглядит качественно одинаково при почти любых масштабах временной оси, имеет память (последействие), а также характеризуется высокой пачечностью. В результате теоретический расчет параметров системы распределения информации, предназначенной для обработки такого трафика, по классическим формулам дает некорректные и неоправданно оптимистические результаты.

Более того, привычные алгоритмы обработки трафика, созданные для работы с простейшими потоками, оказываются недостаточно эффективными для потоков с самоподобием. Таким образом, образовалась проблема самоподобия телетрафика, которой за последние 16 лет посвящено более тысячи работ и которая до сих пор не утратила своей актуальности.

Понятие фрактал было впервые введено Бенуа Мандельбротом в 1975 году. Слово образовано от латинского слова fractus– состоящий из фрагментов. С математической точки зрения фрактальный объект, прежде всего, обладает дробной (нецелой) размерностью.

Известно, что точка имеет размерность, равную нулю. Отрезок прямой и окружность, характеризующиеся протяженностью (длиной), имеют размерность, равную единице. Круг и сфера, характеризующиеся площадью, имеют размерность два. Для описания множества с размерностью 1.5 требуется нечто среднее между длиной и площадью.

Другое важное свойство, которым обладают почти все фракталы – свойство самоподобия(масштабная инвариантность). Фрактал можно разбить на сколь угодно малые части так, что каждая часть окажется просто уменьшенной частью целого. Другими словами, если посмотреть на фрактал в микроскоп, то мы увидим ту же самую картинку, что и без микроскопа (рисунок 8.1). Природа создавала фракталы на протяжении миллионов лет. Фактически большинство объектов в природе – не круги, квадраты или линии.

Рисунок 8.1 - Примеры фрактальных объектов

В самоподобном трафике присутствует некоторое количество достаточно сильных выбросов на фоне относи­тельно низкого среднего уровня, что значительно увеличивает задержки и джиттер при прохождении самоподобного трафика через сеть, даже в случаях, когда средняя интенсивность трафика намного ниже потенциально достижимой скорости передачи в данном канале.

Самоподобные процессы относятся к процессам с длинной памя­тью, что позволяет предсказать их будущее, зная относительно не­давнее прошлое. Заметим, что прогнозирование телетрафика чрез­вычайно важно при разработке алгоритмов работы сетей, обеспечи­вающих повышение качества обслуживания (QoS). Для провайдеров услуг прогнозирование загрузки сетей позволяет планировать их своевременное развитие.

К настоящему времени показано, что самоподобной структурой обладает трафик в проводных сетях при использовании широко распространенных протоколов Ethernet, OKC 7, VoIP, TCP и др. Анало­гичные эффекты обнаружены в сотовых телефонных сетях с комму­тацией пакетов. Опубликованы исследования, результаты которых подтверждают наличие самоподобных свойств и в трафике со­временных телекоммуникационных сетей, использующих технологии беспроводного доступа IEEE 802.116.

В технической литературе вместо термина "фрактальность" иногда используют слово "самоподобность" – перевод с английского "self-similarity". Аналогично, вместо термина "долговременная зависимость" (long-term dependence) употребляется слово "персистентность" (калька с английского "persistence").

Параметр Хёрста.

Для практического выявления свойств фрактальности предложен параметр Хёрста (Hurst). Он назван по фамилии автора этой идеи. Параметр Хёрста (Н) определяет степень самоподобия.

Исследуя по летописям за 800 лет годы разливов Нила, Хэрст обнаружил, что существовала тенденция, когда за годом хорошего на­воднения следовал еще один плодородный год, и, наоборот, за годом малой воды следовал еще один «голодный» год. Другими словами, казалось, что появление голодных и плодородных лет - неслучайно. Для подтверждения данного факта Хэрст ввел коэффициент 0 < Н < 1, который в его честь сейчас называется параметром (экспонентой) Хэрста. В случае независимости друг от друга уровней ежегодных разливов, логично было бы представить процесс разливов обычным броуновским движением с независимыми приращениями, при этом параметр Хэрста Н = 0,5. Однако, как обнаружил Хэрст, для Нила Н = 0,7.

Проверка на самоподобность и оценка показателя Хёрста Н являются сложной задачей. В реальных условиях всегда оперируют с конечными наборами данных, поэтому невозможно проверить, является или нет трафик самоподобным по определению. Следовательно, необходимо исследовать различные свойства самоподобности в реальном измеренном трафике. При этом возникают следующие проблемы.

1. Даже если подтверждаются свойства самоподобности, нельзя сразу делать вывод, что проанализированные данные имеют самоподобную структуру. Следует говорить о самоподобной структуре в заданном масштабном диапазоне для заданного набора данных.

2. Оценка показателя Хёрста зависит от многих факторов, таких как методика оценки, размер выборки, масштаб времени и т.д.

Одним из способов вычисления коэффициента Н является анализ так называемой R/S статистики (нормированного размаха).

Для выборочного случайного набора 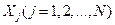определяют выборочное среднее, выборочную дисперсию и интегральное отклонение:

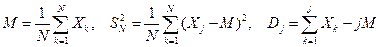. (8.1)

Изменчивость случайного процесса на интервале 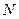определяется как неубывающая функция длины следующего интервала (для ):

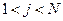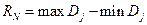. (8.2)

Хёрст показал, что для многих естественных процессов справедливо соотношение такого вида:

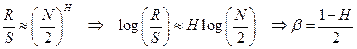. (8.3)

Следует заметить, в случае 0,5 < Н < 1 говорят о персистентном (поддерживающемся) поведении процесса либо о том, что процесс об­ладает длительной памятью. Другими словами, если в течение неко­торого времени в прошлом наблюдались положительные приращения процесса, т.е. происходило увеличение, то и впредь в среднем будет происходить увеличение. Иначе говоря, вероятность того, что процесс на i + 1 шаге отклоняется от среднего в том же направлении, что и на i шаге настолько велика, насколько параметр Н близок к 1. То есть персистентные стохастические процессы обнаруживают четко выражен­ные тенденции изменения при относительно малом «шуме».

В случае 0 < Н < 0,5 говорят об антиперсистентности процесса. Здесь высокие значения процесса следуют за низкими, и наоборот. Дру­гими словами, вероятность того, что на i+ 1 шаге процесс отклоняется от среднего в противоположном направлении (по отношению к отклонению на i шаге) настолько велика, насколько параметр Н близок к 0.

При Н = 0,5 отклонения процесса от среднего являются действи­тельно случайными и не зависят от предыдущих значений, что соот­ветствует случаю броуновского движения.