Уравнение Шредингера. Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях

Уравнением движения в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого вытекали бы волновые свойства частиц. Оно должно быть уравнением относительно волновой функции Ψ(х, у, z, t), так как величина │Ψ│² определяет вероятность пребывания частицы в момент времени в объеме.

Основное уравнение сформулированоЭ. Шредингером: уравнения не выводится, а постулируется.

Уравнение Шредингера имеет вид:

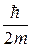- ΔΨ + U(x,y, z, t)Ψ = iħ 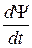, (33.9)

где ħ=h/(2π), т—масса частицы, Δ—оператор Лапласа, i— мнимая единица,U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y, z, t) — искомая волновая функция частицы.

Уравнение (32.9) является общим уравнением Шредингера. Его также называют уравнением Шредингера, зависящим от времени. Для многих физических явлений, происходящих в микромире, уравнение (33.9) можно упростить, исключив зависимость Ψ от времени, иными словами, найти уравнение Шредингера для стационарных состояний — состояний с фиксированными значениями энергии. Это возможно, если силовое поле, в котором частица движется, стационарно, т. е. функцияU(x,y,z,t) не зависит явно от времени и имеет смысл потенциальной энергии.

∆Ψ + 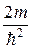(E-U)Ψ = 0. (33.10)

Уравнение (33.10) называется уравнением Шредингера для стационарных состояний.

В это уравнение в качестве параметра входит полная энергия Е частицы. Решение уравнения имеет место не при любых значениях параметра Е, а лишь при определенном наборе, характерном для данной задачи. Эти значения энергии называются собственными. Собственные значения Е могут образовывать как непрерывный и дискретный ряд.

33.5. Частица в одномерной прямоугольной «потенциальной яме с бесконечно высокими «стенками»

Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U (х) = соnstи ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией. Энергия свободной частицы может принимать любые значения, т. е. ее энергетический спектр является непрерывным. Свободная квантовая частица описывается плоской монохроматической волной де Бройля, и все положения свободной частицы в пространстве являются равновероятными.

Проведем качественный анализ решений уравнения Шредингера применительно к свободной частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками» (рис.33.1). Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)

∞, х < 0

U(x) ={0, 0 ≤ х ≤ l}(33.11)

∞, х > 1

где l — ширина «ямы», а энергия отсчитывается от ее дна (рис.33.1).

Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде

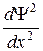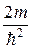+ (Е- U)Ψ =0. (33.12)

По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х=0 и х=l) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид

Ψ(0)=Ψ(l)=0. (33.13)

В пределах «ямы» уравнение Шредингера сведется к уравнению

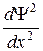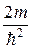+ ЕΨ =0. (33.14)

Стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Е_п зависящих от целого числа п.

Е_п= 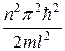,( n= 1, 2, 3, …).(33.15)

Следовательно, энергия Е_п частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения энергии Е_п - называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Е_п, или, как говорят, частица находится в квантовом состоянии п. Частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию меньшую, чем минимальная энергия, равная .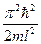

Туннельный эффект

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис.33.2.а) для одномерного (по оси х) движения частицы. Для потенциального барьера прямоугольной формы высоты U ширины l можем записать

0, х < 0(для области 1),

U(x) = {U, 0 ≤ х ≤ l}(для области 2), (33.15)

0, х > 1(для области 3),

При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером (при Е> U), либо отразится от него (при Е< U) и будет двигаться в обратную сторону, т. е. она не может проникнуть сквозь барьер. Для микрочастицы же, даже при Е> U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При Е< U Рис.33.2.

имеется также отличная от нуля вероятность, что частица окажется в области х>l, т. е. проникает сквозь барьер. Подобные, казалось бы, парадоксальные выводы следуют непосредственно из уравнения Шредингера, описывающего микрочастицы при условиях данной задачи.

Таким образом, квантовая механика приводит к специфическому квантовому явлению, получившему название туннельного эффекта, в результате которого микрообъект может «пройти» сквозь потенциальный барьер.

Для описання туннельного эффекта используют понятие коэффициента прозрачности D потенциального барьера, определяемого как отношение плотности потока прошедших частиц к плотности потока падающих.

Решение уравнения Шредингера для прямоугольной потенциального барьера дает формулу для коэффициента прозрачности:

D = D₀ exp( - 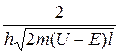), (33.16)

где U — высота потенциального барьера, Е — энергия частицы, l — ширина барьера, D₀— постоянный множитель, который можно приравнять единице. Из этого выражения следует, что D сильно зависит от массы частицы, ширины барьера и от (U - Е); чем шире барьер, тем меньше вероятность прохождения сквозь него частицы.

С классической точки зрения прохождение частицы сквозь потенциальный барьер при Е<U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является специфическим квантовым эффектом. Прохождение частицы сквозь область, в которую, согласно законам классической механики, она не может проникнуть, можно пояснить соотношением неопределенностей. Неопределенность импульса Δр на отрезке Δх=l составляет Δp>h/l. Связанная с этим разбросом в значениях импульса кинетическая энергия может сказаться достаточной для того, чтобы полная энергия частицы сказалась больше потенциальной.

Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например, явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например, a-распад, протекание термоядерных реакций).