Следствия из преобразований Лоренца

Длительность событий в разных системах отсчета.Пусть в некоторой точке (с координатой х), покоящейся относи­тельно системы К, происходит событие, длительность которого (разность показа­ний часов в конце и начале события) τ = t₂ – t₁, где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К′

τ' = t'₂ - t′₁,(5.6)

причем началу и концу события, согласно (5.5), соответствуют

t′₁ = 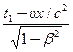, t′₂ = 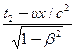. (5.7)

Подставляя (5.7) в (5.6), получаем

τ′ = (t₂ – t₁)/ 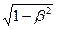= τ/ 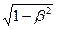. (5.8)

Из соотношения (5.8) вытекает, что τ < τ', т. е. длительность события, проис­ходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, отно­сительно которой эта точка неподвижна. Этот результат может быть еще истолко­ван следующим образом: интервал време­ни τ', отсчитанный по часам в системе К', с точки зрения наблюдателя в системе К, продолжительнее интервала τ, отсчитан­ного по его часам. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоя­щихся часов, т. е. ход часов замедляется в системе отсчета, относительно которой часы движутся.

Длина тел в разных системах отсче­та.Рассмотрим стержень, расположенный вдоль оси х' и покоящийся относительно системы К'. Длина стержня в системе К' будет l′₀ = x′₂ - х'₁, где х'₁и x′₂ - не изменя­ющиеся со временем t′ координаты начала и конца стержня, а индекс 0 показывает, что в системе отсчета К' стержень покоит­ся. Определим длину этого стержня в системе К, относительно которой он движется со скоростью υ. Для этого необхо­димо измерить координаты его концов х₁и x₂в системе К в один и тот же момент времени t. Их разность l = х₂ – x₁и даст длину стержня в системе К. Используя преобразования Лоренца (5.5), полу­чим

l′₀ = x′₂ - х'₁ = - 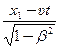= = 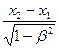l/ 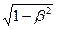. (5.9)

Таким образом, длина стержня, измерен­ная в системе, относительно которой он движется, оказывается меньше длины, из­меренной в системе, относительно которой стержень покоится. Если стержень покоит­ся в системе К, то, определяя его длину в системе К', опять-таки придем к выраже­нию (5.9).

Из выражения (5.9) следует, что ли­нейный размер тела, движущегося относи­тельно инерциальной системы отсчета, уменьшается в направлении движения в 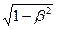раз, т. е. так называемое лоренцево сокращение длинытем больше, чем больше скорость движения.