ВЫЧИСЛИТЕЛЬНЫЕ СХЕМЫ НА ОСНОВЕ ОПЕРАЦИОННЫХ УСИЛИТЕЛЕЙ

Современные компьютеры позволяют с высокой точностью выполнять любые математические операции с числами. Однако на практике часто приходится оперировать с величинами, представленными в виде напряжения или тока. Так, большинство датчиков различных физических величин дают информацию об измеряемом параметре именно в таком виде. В этих случаях, чтобы использовать компьютер, приходится применять аналого-цифровые и цифроаналоговые преобразователи. Конечно, такие системы достаточно сложные и дорогостоящие, что не всегда экономически оправдано.

Аналоговая схемотехника на основе операционных усилителей позволяет создавать самые различные вычислительные схемы весьма просто и эффективно. На основе операционных усилителей могут быть реализованы четыре основных действия арифметики, операции дифференцирования и интегрирования, трансцендентные функции. Недостатком этих вычислительных схем является невысокая точность вычислений — не более 0,1 %. Однако этой точности в целом ряде случаев бывает вполне достаточно.

Схема суммирования

Для суммирования нескольких напряжений можно применить операционный усилитель в инвертирующем включении (рис. 2.15, а). Входные напряжения через резисторы R₁...R_n подаются на инвертирующий вход усилителя, который в этой схеме является суммирующей точкой. Поскольку эта точка является виртуальным нулем (неинвертирующий вход заземлен, а ΔU_вх ≈ 0), то токи, создаваемые входными напряжениями, будут суммироваться и течь через резистор R_ос:

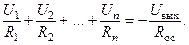
Если все резисторы взять одинаковыми, то

.

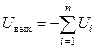Суммирование входных напряжений можно также проводить с любым постоянным смещением. Для этого на один из входов подается постоянное напряжение смещения.

Схема вычитания

На рис. 2.15, б изображена схема, обеспечивающая вычитание двух напряжений:

U_вых = U₂ – U₁.

Если все сопротивления сделать одинаковыми, то при отсутствии второго напряжения, т.е. U₂ = 0, остается схема с инвертирующим включением усилителя (см. рис. 2.14, а), для которого

.

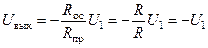При отсутствии первого напряжения, т.е. U₁ = 0, усилитель должен создать на выходе такое напряжение U_вых, чтобы потенциалы на инвертирующем и неинвертирующем входах были бы равны. Потенциал на неинвертирующем входе равен:

.

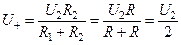Потенциал на инвертирующем входе (см. рис. 2.14, б) равен:

.

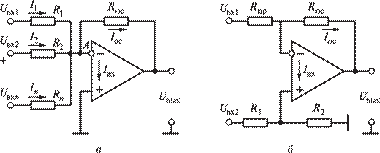
Рис. 2.15. Схемы суммирования (а) и вычитания (б)

Таким образом, U_вых = U₂. Если же на обоих входах присутствуют сигналы, то U_вых = U₂ – U₁. Изменяя соотношение сопротивлений в делителях таким образом, чтобы R_пр = R_ос/α, R₁ = R₂/α, а R_ос = R₂, операцию вычитания можно выполнять с коэффициентом α:

U_вых = α (U₂ – U₁).

Наконец, если во входных цепях инвертирующего и неинвертирующего входов включить схемы, подобные входной схеме суммирующего усилителя и через резисторы подключить параллельно несколько входных напряжений, можно получить схему сложения и вычитания большого числа сигналов:

U_вых = αΣU_i – βΣU_j,

где U_i — сигналы в цепи неинвертирующего входа, а U_j — в цепи инвертирующего входа.