Модели некооперированной олигополии

При некооперированной олигополии фирмы, стремясь к максимизации прибыли, действуют независимо, на свой страх и риск. В соответствии с этим делением классифицируют и модели олигополий.

В качестве моделей некооперированной олигополиивыступают: модель Курно, модель Штакельберга, модель ломаной кривой спроса.

Первая модель была предложена французским математиком А. О. Курно. Курно исходил из того, что:

· обе фирмы производят однородный товар;

· им известна кривая рыночного спроса;

· обе фирмы принимают решения о производстве одновременно, причем самостоятельно и независимо друг от друга;

· каждая из фирм предполагает выпуск конкурента постоянным;

· продавцы не могут иметь точной информации о своих ошибках относительно выбранных объемов производства. Фактически же эти предположения продавцов о реакции конкурента, очевидно, изменятся, когда они узнают о своих предыдущих ошибках.

Модель Курно представлена на рисунке 110.

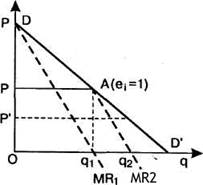
Рисунок 110 - Модель дуополии Курно

Предположим, что первым начинает производство дуополист 1, который в первое время оказывается монополистом. Его выпуск составляет q1, что при цене Р позволяет ему извлекать максимальную прибыль, ибо в этом случае MR = = МС = 0. При данном объеме выпуска эластичность рыночного спроса равна единице, а общая выручка достигнет максимума. Затем производство начинает дуополист 2. В его представлении объем выпуска сдвинется вправо на величину Oq1 и совместится с линией Aq1. Сегмент AD' кривой рыночного спроса DD он воспринимает как кривую остаточного спроса, которой соответствует кривая его предельной выручки MR2. Выпуск дуополиста 2 будет равен половине неудовлетворенного дуополистом 1 спроса, т. е. сегмента q1D', а величина его выпуска равна q1q2, что даст возможность получить максимум прибыли. Данный выпуск составит четверть всего рыночного объема спроса при нулевой цене, OD'(1/2 x 1/2 = 1/4).

На втором шаге дуополист 1, допуская, что выпуск дуополиста 2 сохранится стабильным, решит покрыть половину оставшегося все еще неудовлетворенным спроса. Исходя из того что дуополист 2 покрывает четверть рыночного спроса, выпуск дуополиста 1 на втором шаге составит (1/2)x(1- 1/4), т.е. 3/8 всего рыночного спроса, и т. д. С каждым последующим шагом выпуск дуополиста 1 будет уменьшаться, в то время как выпуск дуополиста 2 будет увеличиваться. Такой процесс окончится уравновешиванием их выпуска, и тогда дуополия достигнет состояния равновесия Курно.

Модель Курно многие экономисты считали наивной по следующим основаниям. Модель допускает, что дуополисты не делают никаких выводов из ошибочности своих предположений относительно реакции конкурентов. Модель закрыта, т. е. число фирм ограничено и не меняется в процессе движения к равновесию. Модель ничего не говорит о возможной продолжительности этого движения. И наконец, нереальным представляется предположение о нулевых операционных издержках. Равновесие в модели Курно можно изобразить через кривые реагирования, показывающие максимизирующие прибыль объемы выпуска, который будет осуществляться одной фирмой, если даны объемы выпуска конкурента.

На рисунке 111 кривая реагирования I представляет максимизирующий прибыль выпуск первой фирмы как функцию от выпуска второй. Кривая реагирования II представляет максимизирующий прибыль выпуск второй фирмы как функцию от выпуска первой.

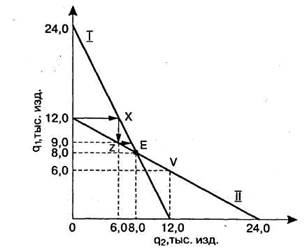
Рисунке 111 - Кривые реагирования

Кривые реагирования можно использовать для того, чтобы показать, как устанавливается равновесие. Если следовать стрелкам, нарисованным от одной кривой к другой, начиная с выпуска q1 = 12 000, то это приведет к осуществлению равновесия Курно в точке Е, в которой каждая фирма производит 8000 изделий. В точке Е пересекаются две кривые реагирования. Это и есть равновесие Курно.

Модель Курно при всех своих достоинствах, с момента своего появления вызвала немало критики. Данную модель обвиняли в чрезмерной упрощенности и нереалистичности ее исходных допущений, поскольку в модели Курно:

- олигополисты не предполагают возможность изменения объемов выпуска своих конкурентов;

- поведение фирм на рынке совершенно одинаково (симметрично). Между тем на практике олигополисты могут придерживаться различных типов поведения.

Модель асимметричной олигополии была предложена немецким экономистом Г. фон Штакельбергом (Henrich von Stackelberg, Marktform und Gleichgewicht, 1934). Эта модель развивает идеи Курно. Так же как и в модели Курно каждое предприятие выбирает оптимальный объем производства, но Штакельберг выдвигает новую гипотезу: на рынке могут существовать дуополист-лидер и дуополист-последователь.

Последователь придерживается предположения Курно, он принимает решения об оптимальном объеме выпуска в соответствии со своей кривой реакции, полагая объем выпуска конкурента заданным и приспосабливая свое производство к этому объему. Лидер, напротив, играет доминирующую роль на рынке. Он понимает, что другая фирма ведет себя как последователь, и зная кривую реакции этой фирмы, принимает свои решения об объеме выпуска по сути как монополист.

Сравнение равновесия Курно и равновесия Штакельберга показывает, что позиция фирмы-лидера более предпочтительна, чем в симметричной ситуации модели Курно, однако если обе фирмы стремятся стать лидерами, это ведет к агрессивной конкуренции и ценовой войне, которая может привести к снижению цен до конкурентного уровня и будет продолжаться до тех пор, пока одна из фирм не откажется от своих притязаний.

Модель ломаной кривой спроса была разработана в 1939 г. экономистом Полем Свизи (Paul Sweezy. Demand under Conditions of Oligopoly // Journal of Political Economy,1939.Vol.47.Aug.). Основная задача автора модели — объяснить жесткость цен в условиях некооперируемой олигополии.

Предположим, что три крупных фирмы А, В и С производят практически однородный товар и владеют каждая 1/3 рынка. Все три фирмы продают свою продукцию по общей цене P*. Объем продаж фирмы А при данной цене составляет Q*. Как отреагируют олигополисты В и С, если фирма А в одностороннем порядке решит изменить цены на свою продукцию?

Если фирма А понижает свои цены ниже уровня сложившейся цены Р*, то ее конкуренты скорее всего последуют ее примеру, чтобы не потерять своих покупателей и не допустить укрепления фирмы А за их счет.

Если фирма А повышает свои цены выше сложившейся в отрасли цены Р*, то скорее всего фирмы В и С не последуют ее примеру, поскольку, в этом случае они, ничего не предпринимая, расширят свои доли рынка за счет части покупателей фирмы А.

Можно предположить, что если на олигопольном рынке конкуренты игнорируют повышение цен, но реагируют соответствующим образом на понижение цен, то кривая спроса фирмы А будет иметь различный наклон выше и ниже уровня преобладающей цены. Перегиб кривой спроса в точке преобладающей цены имеет своим следствием разрыв кривой предельного дохода на участке ВС, как это представлено на рисунке 112.

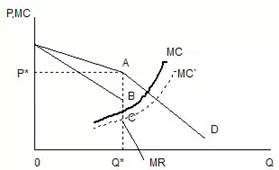
Рисунок 112 - Модель ломаной кривой спроса (рост издержек)

Предположим, что кривая предельных издержек МС фирмы проходит через разрыв ВС. Как видно из приведенного рисунка, оптимальный объем производства равен Q*, а оптимальная цена Р*. Если по каким-то причинам издержки возрастают и кривая МС смещается вправо в пределах отрезка ВС (например, в положение МС`), то ни оптимальный объем, ни оптимальная цена не поменяются.

Аналогичным образом можно рассмотреть ситуацию, когда меняется рыночный спрос. Как видно из рисунке 113, увеличение рыночного спроса и соответствующее смещение кривой предельного дохода вызовут прирост оптимального объема, но сохранят неизменной рыночную цену.

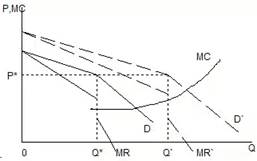
Рисунок 113 - Модель ломаной кривой спроса (рост спроса)

Модель ломаной кривой спроса, по мысли ее создателя, позволяет объяснить причину стабильности цен на олигопольном рынке при небольшом изменении издержек или рыночного спроса на продукцию. Очевидно, что если конкуренты ожидают адекватной реакции на свои действия, то они постараются воздерживаться от одностороннего повышения или понижения цен.

Исключением может быть ситуация, когда издержки олигополистов существенно отличаются друг от друга, и фирма с наименьшими издержками может назначить более низкую цену, чтобы использовать данное преимущество. Более того, поскольку покупатели могут достаточно легко поменять продавца, выбирая того, у кого цены ниже, конкуренция заставляет олигополистов продавать свою продукцию по одинаковым или почти одинаковым ценам. Исключением является дифференцированная олигополия. Если фирма сформировала высокую приверженность своей торговой марке среди покупателей, то они будут готовы платить более высокую цену за покупку более качественного товара.

Практические наблюдения не противоречат выводам из данной модели. Результаты исследований показывают, что в чистой или слабо дифференцированной олигополии существует тенденция к выравниванию цен (рынок алюминия, цемента, стали), в отраслях же сильно дифференцированных олигополисты взимают сопоставимые цены.

Вместе с тем допущение о возможной реакции конкурентов не всегда справедливо.

Понижение цены одним из олигополистов может быть расценено не как попытка ценовой конкуренции, а следствием того, что:

- товар устарел и возникли проблемы с его сбытом;

- фирма находится в сложном финансовом положении и пытается расширить рынок сбыта. Соответственно и реакции конкурентов будут зависеть от их видения ситуации.

С другой стороны, тенденция игнорирования повышения цены не действует в условиях инфляции, когда в течение некоторого периода наблюдается повышение общего уровня цен в экономике.

Или когда в отрасли имеют место серьезные изменения в отраслевых издержках или рыночном спросе.

10.2 Олигополия с точки зрения теории игр. "Дилемма заключенного"

В настоящее время все большее значение для анализа олигополистических ситуаций получает теория игр. Теория игр — наука, исследующая математическими методами поведение участников в вероятностных ситуациях, связанных с принятием решений. Предметом этой теории являются игровые ситуации с заранее установленными правилами (типа игры в карты или в домино). В ходе игры возможны различные совместные действия — коалиции игроков, конфликты и т. д. Стратегия игроков определяется целевой (платежной) функцией, которая показывает выигрыш или проигрыш участника Формы этих игр многообразны. Наиболее простая разновидность — игры с двумя участниками. Если в игре участвуют не менее трех игроков, возможно образование коалиций, что усложняет анализ С точки зрения платежной суммы игры делятся на две группы — с нулевой и ненулевой суммами Игры с нулевой суммой называют еще антагонистическими: выигрыш одних в точности равен проигрышу других, а общая сумма выигрыша равна нулю. По характеру предварительной договоренности игры делятся на кооперативные (когда образуются коалиции игроков) и некооперативные (когда каждый играет за себя против всех).

Наиболее известный пример некооперативной игры с нулевой суммой — модель Курно, а с ненулевой суммой — "дилемма заключенного".

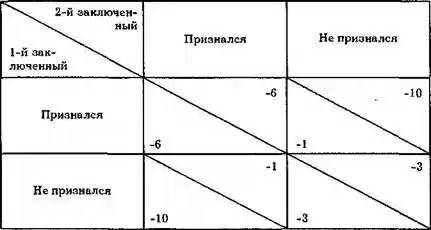
Рассмотрим последний случай (Таблица 3). С поличным поймали двух воров, которым предъявлено обвинение в ряде краж. Перед каждым из них встает дилемма — признаваться ли в старых (недоказанных) кражах или нет. Если признается только один из воров, то признавшийся получает минимальный срок заключения (1 год), а его нераскаявшийся товарищ — максимальный (10 лет). Если оба вора одновременно признаются, то оба получат небольшое снисхождение (по 6 лет заключения), если оба будут упорствовать, то обоим дадут наказание только за последнюю кражу (по 3 года). Заключенные сидят в разных камерах и не могут договориться друг с другом. Перед нами — некооперативная (несогласованная) игра с ненулевой (в данном случае отрицательной) суммой Характерной чертой этой игры является невыгодность для обоих участников руководствоваться своими частными (корыстными) интересами.

Таблица 3 "Дилемма заключенного"