Определение оптимального объема выпуска

При совершенной конкуренции текущая цена устанавливается рынком, и отдельная фирма не может воздействовать на нее, поскольку является ценополучателем. В этих условиях единственный способ увеличения прибыли состоит в регулировании объема выпуска.

Исходя из существующих в данный момент времени рыночных и технологических условий, фирма определяет оптимальный объем выпуска, т.е. объем выпуска, обеспечивающий фирме максимизацию прибыли (или минимизацию издержек, если получение прибыли невозможно).

Существует два взаимосвязанных метода определения точки оптимума:

1. Метод совокупных издержек — совокупного дохода.

Совокупная прибыль фирмы максимизируется при таком объеме выпуска, когда разница между TR и TC будет максимально большой.

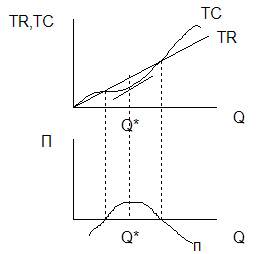
Рисунок 74 - Определение точки оптимального производства

На рисунке 74 оптимизирующий объем находится в точке, где касательная к кривой ТС имеет тот же наклон, что и кривая ТR. Функция прибыли находится путем вычитания ТС из ТR для каждого объема производства. Пик кривой совокупной прибыли (п) показывает объем выпуска, при котором прибыль максимальна в краткосрочном периоде.

Из анализа функции совокупной прибыли следует, что совокупная прибыль достигает своего максимума при объеме производства, при котором ее производная равна нулю, или dп/dQ=(п)`= 0.

Производная функции совокупной прибыли имеет строго определенный экономический смысл — это предельная прибыль.

Предельная прибыль (Mп) показывает прирост совокупной прибыли при изменении объема выработки на единицу.

Если Мп>0, то функция совокупной прибыли растет, и дополнительное производство может увеличить совокупную прибыль.

Если Мп<0, то функция совокупной прибыли уменьшается, и дополнительный выпуск сократит совокупную прибыль.

И, наконец, если Мп=0, то значение совокупной прибыли максимально.

Из первого условия максимизации прибыли (Мп=0) вытекает второй метод.

2. Метод предельных издержек — предельного дохода. Мп=(п)`=dп/dQ, (п)`=dTR/dQ-dTC/dQ.

А поскольку dTR/dQ=MR, а dTC/dQ=МС, то совокупная прибыль достигает своего наибольшего значения при таком объеме выпуска, при котором предельные издержки равны предельному доходу: MC=MR

Если предельные издержки больше предельного дохода (МC>МR), то предприятие может увеличить прибыль за счет сокращения объема производства. Если предельные издержки меньше предельного дохода (МC<МR), то прибыль может быть увеличена за счет расширения производства, и лишь при МС=МR прибыль достигает своего максимального значения, т.е. устанавливается равновесие.

Данное равенство действует для любых рыночных структур, однако в условиях совершенной конкуренции оно несколько модифицируется.

Поскольку рыночная цена тождественна среднему и предельному доходам фирмы — совершенного конкурента (РAR=MR), то равенство предельных издержек и предельных доходов трансформируется в равенство предельных издержек и цены: MC=P.

Пример 1. Нахождение оптимального объема выпуска в условиях совершенной конкуренции.

Фирма действует в условиях совершенной конкуренции. Текущая рыночная цена Р=20 у.е. Функция совокупных издержек имеет вид ТС=75+17Q+4Q2.

Требуется определить оптимальный объем выпуска.

Решение (1 способ):

Для нахождения оптимального объема, вычислим MC и MR, и приравняем их друг к другу.

1. МR=P*=20.

2. МС=(ТС)`=17+8Q.

3. MC=MR.

20=17+8Q.

8Q=3.

Q=3/8.

Таким образом, оптимальный объем составляет Q*=3/8.

Решение (2 способ):

Оптимальный объем может быть найден и через приравнивание предельной прибыли нулю.

1. Находим совокупный доход: TR=Р*Q=20Q

2. Находим функцию совокупной прибыли:

п=TR-TC,

п=20Q-(75+17Q+4Q2)=3Q-4Q2-75.

3. Определяем функцию предельной прибыли:

Мп=(п)`=3-8Q, а затем приравниваем Мп к нулю.

3-8Q=0;

Q=3/8.

Решая это уравнение, мы получили тот же самый результат.