Энергия гармонического осциллятора

Рассмотрим материальную точку с массой 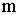, на которую действует квазиупругая сила 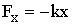. Потенциальная и кинетическая энергии точки равны

,

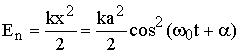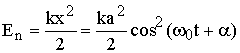, т.е.

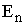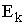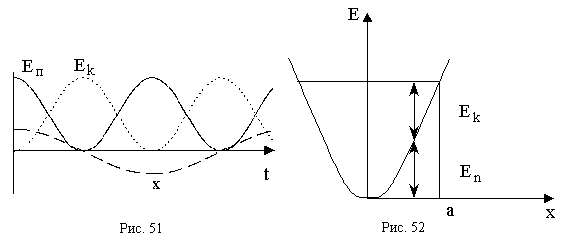
и сдвинуты друг относительно друга по фазе на (рис. 51).

Полная энергия материальной точки сохраняется

( );

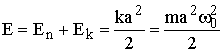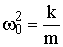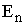переходит в 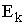и наоборот (рис. 51, 52),

а средняя энергия 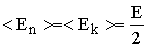, т.к. средние значения 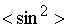и 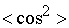за период равны .

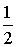Уравнение движения можно получить из закона сохранения энергии: для этого уравнение для энергии дифференцируется по 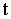и ( ).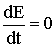

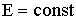Энергетический критерий малых колебаний:

,

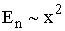где 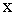- смещение из положения равновесия. В этом случае колебания можно считать гармоническими.

КВАЗИУПРУГАЯ СИЛА - направленная к центру О сила. модуль к-рой пропорционален расстоянию r от центра О до точки приложения силы (F=-cr), где с - постоянный коэф., численно равный силе, действующей на единице расстояния. К. с. является силой центральной и потенциальной с силовой ф-цией U=-0,5cr². Примерами К. с. служат силы упругости, возникающие при малых деформациях упругих тел (отсюда и сам термин "К. с."). Приближённо К. с. можно также считать касательную составляющуюсилы тяжести, действующей на матем. маятник при малых его отклонениях от вертикали. Для материальной точки, находящейся под действием К. с., центр О является положением её устойчивого равновесия. Выведенная из этого положения точка будет в зависимости от нач. условий или совершать около О прямолинейные гармонич. колебания, или описывать эллипс (в частности, окружность).