Динамика гармонических колебаний. Итак, чтобы определить подчиняется ли рассматриваемое движение закону гармонических колебаний, необходимо уравнение движения привести к виду и определить из

Итак, чтобы определить подчиняется ли рассматриваемое движение закону гармонических колебаний, необходимо уравнение движения привести к виду 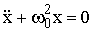и определить 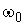из коэффициента при 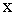. Рассмотрим примеры движения механических систем.

1. Пружинный гармонический маятник (осциллятор)

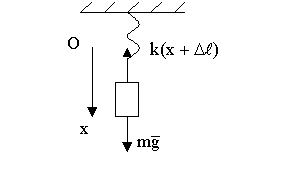Груз (рис. 48) подвешен на невесомой пружине с коэффициентом жесткости 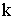и совершает вертикальные колебания относительно т. - положения равновесия. По второму закону Ньютона в этом положении

,

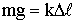где 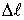- растяжение пружины,

а при отклонении из положения равновесия

, т.е.

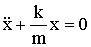
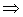
частота и период осциллятора соответственно равны

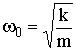и .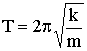

2. Математический маятник

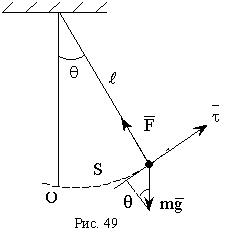
Это идеализированная система, представляющая собой материальную точку с массой 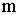, подвешенную на нерастяжимой нити длиной 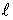и совершающую колебания в вертикальной плоскости (рис. 49).

Опишем движение естественным способом. Точка 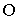отвечает положению равновесия, и тогда

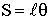и соответственно

.

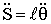Проекция силы натяжения на касательное направление 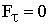, т.е.

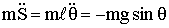и

.

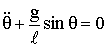При малых колебаниях 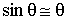и

, .

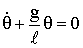
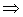
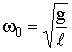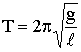3.Физический маятник

Это твердое тело, которое совершает колебания вокруг неподвижной оси, жестко связанной с телом.

Рассмотрим колебания под действием силы тяжести (рис. 50). Угол 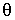показывает поворот против часовой стрелки, ось 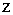направлена от плоскости чертежа.

Проекция момента силы тяжести на ось 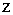равна

,

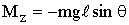и тогда уравнение динамики вращательного движения принимает вид

,

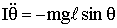где 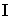- момент инерции относительно оси O,

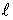- расстояние между O и центром масс.

При малых колебаниях 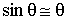и

, .

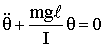
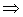
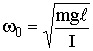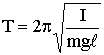Здесь 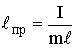- приведенная длина физического маятника, равная длине математического маятника с такой же 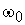. Если 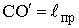, то т. 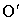называется центром качания, особенностью которого является, что если маятник перевернуть и колебать относительн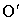о , то 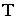не изменится принцип определения 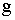с помощью оборотного маятника.

Повторим, что малые поворотные колебания являются гармоническими ввиду того, что действующая в осцилляторе сила квазиупруга, то есть направлена к положению равновесия и зависит от смещения от этого положения линейно, но имеет другую природу, чем упругие силы.

Параметры 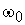и 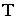свободных колебаний без трения зависят от свойств осциллятора; 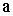и 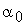-определяются начальными условиями.