Кинематика гармонического колебания

Кинематика гармонического колебания.

Процессы, повторяющиеся во времени называются колебаниями.

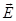В зависимости от природы колебательного процесса и механизма возбуждения бывают: механические колебания (колебания маятников, струн, зданий, земной поверхности и т.д.); электромагнитные колебания (колебания переменного тока, колебания векторов и 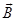в электромагнитной волне и т.д.); электромеханические колебания (колебания мембраны телефона, диффузора громкоговорителя и др.); колебания ядер и молекул в результате теплового движения в атомах.

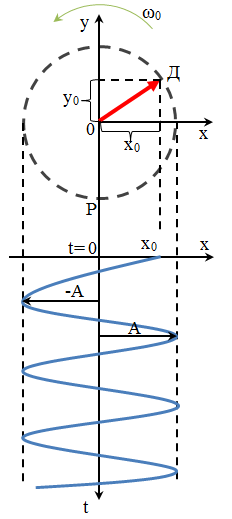
Рассмотрим отрезок [ОД] (радиус-вектор), совершающий вращательное движение вокруг точки 0. Длина |ОД| = A. Вращение происходит с постоянной угловой скоростью ω₀. Тогда угол φ между радиус-вектором и осью x меняется со временем по закону

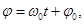
где φ₀ - угол между [ОД] и осью х в момент времени t = 0. Проекция отрезка [ОД] на осьх в момент времени t = 0

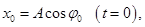
а в произвольный момент времени

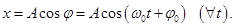(1)

Таким образом, проекция отрезка [ОД] на ось х совершает колебания, происходящие вдоль оси х, и эти колебания описываются законом косинуса (формула (1)).

Колебания, которые описываются законом косинуса

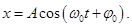
или синуса

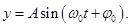
называется гармоническими.

Гармонические колебания являются периодическими, т.к. значение величины х (и у) повторяется через равные промежутки времени.

Если отрезок [ОД] находится з низшем положении по рисунку, т.е. точка Д совпадает с точкой Р, то его проекция на ось х равна нулю. Назовем такое положение отрезка [ОД] положением равновесия. Тогда можно сказать, что величина х описывает смещение колеблющейся точки из положения равновесия. Максимальное смещение от положения равновесия называется амплитудой колебания

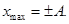
Величина

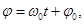
которая стоит под знаком косинуса называется фазой. Фаза определяет смещение от положения равновесия в произвольный момент времени t. Фаза в начальный момент времени t = 0, равная φ₀ называется начальной фазой.

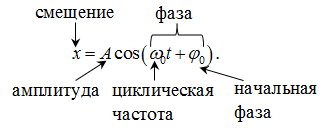Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.

Промежуток времени, за который совершается одно полное колебание, называется периодом колебаний Т. Число колебаний в единицу времени называется частотой колебаний ν.

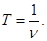
Через промежуток времени, равный периоду Т, т.е. при увеличении аргумента косинуса на ω₀Т, движение повторяется, и косинус принимает прежнее значение

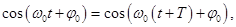
т.к. период косинуса равен 2π , то, следовательно, ω₀Т = 2π

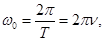
таким образом, ω₀ - это число колебаний тела за 2π секунд. ω₀ - циклическая или круговая частота.

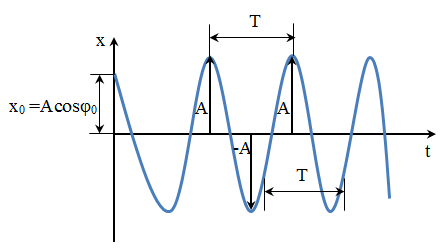
рисунок гармонического колебания

А - амплитуда, Т – период, х - смещение, t – время.

Скорость колеблющейся точки найдем, продифференцировав уравне­ние смещения х(t) по времени

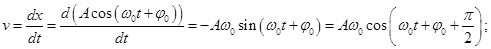
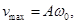
т.е. скорость v отличается по фазе от смещения х на π/2.

Ускорение - первая производная от скорости (вторая производная от смещения) по времени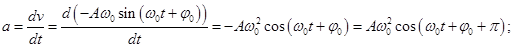

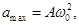
т.е. ускорение а отличается от смещения по фазе на π.

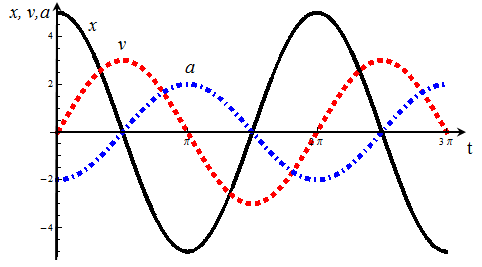
Построим график х(t), у(t) и а(t) в одной смете координат (для простоты примем φ₀= 0 и ω₀ = 1)

Свободными или собственными называются колебания, которые происходят в системе предоставленной самой себе после того, как она была выведена из положения равновесия