Решение типовых задач
Задача 1. Данные об источниках денежных доходов населения в текущих ценах, млрд. руб., приведены в таблице:
| Показатель | Год | |
| Денежные доходы: доходы от предпринимательской деятельности оплата труда социальные выплаты доходы от собственности другие доходы | 1 280,4 6 885,1 1 516,6 780,5 235,9 | 1 606,8 8 653,4 1 720,8 1 103,1 292,8 |
| Денежные расходы и сбережения: на покупку товаров и оплату услуг на обязательные платежи и разные взносы на приобретение недвижимости на прирост финансовых активов | 7 382 885,8 224,7 2 206 | 9 330,4 1 225,3 2 508,2 |
| Индекс потребительских цен,% |
Определить:
1. номинальные и располагаемые денежные доходы населения в текущих ценах;
2. индексы номинальных и располагаемых денежных доходов населения;
3. реальные располагаемые денежные доходы населения;
4. индекс реальных располагаемых денежных доходов населения.
Решение:
1. Номинальные доходы населения составили:
в 2010 г.: 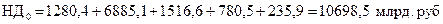
в 2011 г.: 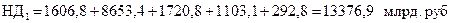
Располагаемые денежные доходы населения составили:
в 2010 г.: 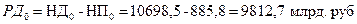
в 2011 г.: 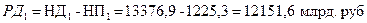
2. Индекс номинальных денежных доходов населения:
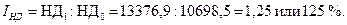
Индекс располагаемых денежных доходов населения:
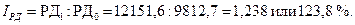
Номинальные денежные доходы населения в 2011 г. по сравнению с 2010 г. выросли на 25%, располагаемые денежные доходы – на 23,8%.
3. Реальные располагаемые денежные доходы населения составили:
в 2010 г.: 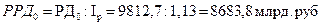
в 2011 г.: 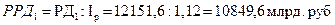
4. Индекс реальных располагаемых денежных доходов населения:
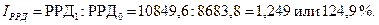
Реальные располагаемые денежные доходы населения в 2011 г. по сравнению с 2010 г. выросли на 24,9%.
Задача 2. Данные об источниках денежных доходов населения Российской Федерации в текущих ценах приведены в таблице:
| Источники денежных доходов | Удельный вес,% к итогу | |
| 3 квартал 2011 г. | 3 квартал 2012 г. | |
| Денежные доходы, всего | 100,0 | 100,0 |
| В том числе: доходы от предпринимательской деятельности оплата труда социальные выплаты доходы от собственности другие доходы | 10,4 66,7 12,8 8,1 2,0 | 8,9 66,3 19,2 3,6 2,0 |
Определить: Интегральный коэффициент структурных различий К. Гатева, коэффициент А. Салаи.
Решение:
Для определения коэффициентов Гатева и Салаи построим вспомогательную таблицу:
| Источники денежных доходов | 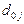
| 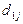
| 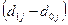
| 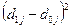
| 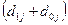
| 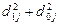
| 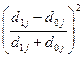
|
| Доходы от предпринимательской деятельности | 10,4 | 8,9 | -1,5 | 2,25 | 19,3 | 187,37 | 0,00604 |
| Оплата труда | 66,7 | 66,3 | -0,4 | 0,16 | 8 844,58 | 0,000009 | |
| Социальные выплаты | 12,8 | 19,2 | 6,4 | 40,96 | 532,48 | 0,04 | |
| Доходы от собственности | 8,1 | 3,6 | -4,5 | 20,25 | 11,7 | 78,57 | 0,147929 |
| Другие доходы | 2,0 | 2,0 | |||||
| Итого | 63,62 | 0,193978 |
Интегральный коэффициент структурных сдвигов Гатева:
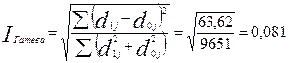 .
.
Индекс структурных различий Салаи определяется по формуле:
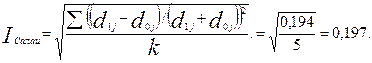
Вычисленные значения критериев показывают, что наблюдается низкий уровень различий структур источников денежных доходов в 2011 и 2012 гг.
Задача 3. Рассчитаем коэффициент Джини на основе данных о распределении общего объема денежных доходов населения России в 2009 г. по квинтильным группам:
| 20-ти процентные группы населения | Денежныe доходы населения, в% к итогу |
| первая (с наименьшими доходами) | 5,3 |
| вторая | |
| третья | |
| четвертая | 22,6 |
| пятая (с наивысшими доходами) | 47,1 |
| Итого |
Решение:
Для исчисления коэффициента Джини необходимо рассчитать величины  и
и 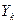 . В каждой из выделенных групп находится по 20% населения, что в долях единицы составляет 0,2.
. В каждой из выделенных групп находится по 20% населения, что в долях единицы составляет 0,2.
Соответственно получаем:
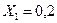 ;
; 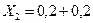 ;
; 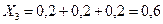 ;
; 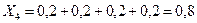 ;
; 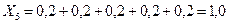
По такой же схеме рассчитывается величина 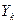 , но при этом используются данные о кумулятивных удельных весах каждой группы в общем объеме денежных доходов населения:
, но при этом используются данные о кумулятивных удельных весах каждой группы в общем объеме денежных доходов населения:
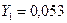 ;
; 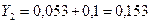 ;
; 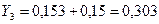 ;
; 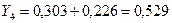 ;
; 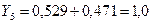
Полученные результаты представим в виде вспомогательной таблицы (таблица 6.2), в которой проведем расчет величин 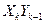 и
и 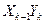 .
.
Таблица 6.2

| 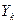
| 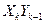
| 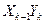
|
| 0,2 | 0,053 | 0,0306 | - |
| 0,4 | 0,153 | 0,1212 | 0,0212 |
| 0,6 | 0,303 | 0,3174 | 0,0918 |
| 0,8 | 0,529 | 0,8 | 0,2424 |
| 1,0 | 1,0 | - | 0,529 |
| Итого | - | 1,2692 | 0,8844 |
Соответственно коэффициент Джини равен:
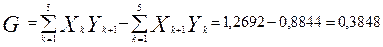
Для справки, коэффициент Джини, рассчитанный для 2006 года, составлял 0,3812. Если сравнить коэффициенты за 2 года, то можно сказать об увеличении концентрации доходов в отдельных группах населения, т.е. об увеличении неравенства населения по доходам.
Задача 4. На основании данных задачи 3. построить кривую Лоренца и рассчитать на ее основе коэффициент Джини.
Решение: Построим вспомогательную таблицу для расчетов (таблица 6.3)
Таблица 6.3
Кумулятивные доли населения,%

| Доли доходов населения,%
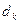
| Кумулятивные доли доходов населения,%
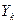
| Площадь фигуры под кривой Лоренца
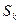
|
| 5,3 | 5,3 | ||
| 15,3 | |||
| 30,3 | |||
| 22,6 | 52,9 | ||
| 41,7 | 1 529 | ||
| Итого | - | 3 076 |
Площадь первой фигуры под кривой Лоренца определим по формуле:
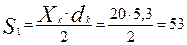 ;
;
Площадь второй и последующих фигур исчислим по формуле:
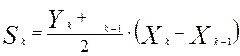 .
.
Например, 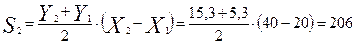 .
.
Определим таким способом площади всех фигур и результаты поместим в последнюю колонку таблицы. Сумма всех площадей равна общей площади фигуры под кривой Лоренца. В данном случае, общая площадь равна 3076.
Очевидно, что площадь фигуры (треугольника) под линией общего равенства равна 5000. Исходя из этого, найдем коэффициент Джини по формуле:
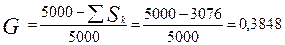 . Отразим кривую Лоренца на графике (рис. 6.2).
. Отразим кривую Лоренца на графике (рис. 6.2).
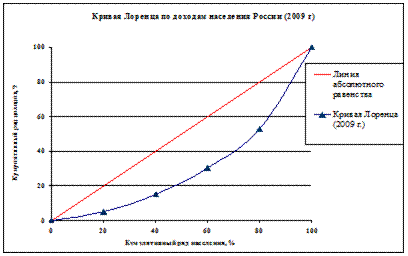
Рис. 6.2 Кривая Лоренца по доходам населения России в 2009 году.
Задача 5. В результате выборочного обследования 100 семей по размеру месячного дохода на одного члена семьи была получена следующая группировка:
| Группы семей по доходу на одного члена семьи, тыс. руб. на человека | Средний размер дохода, тыс. руб.,
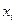
| Число семей,
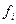
| Средний размер разовой покупки, тыс. руб.
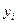
| Прирост доходов, тыс. руб.
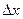
| Прирост размера покупки
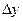
|
| До 10 | 0,5 | - | - | ||
| 10-15 | 12,5 | 0,7 | 7,5 | 0,2 | |
| 15-25 | 7,5 | 0,3 | |||
| 25-40 | 32,5 | 12,5 | |||
| 40-60 | 17,5 | ||||
| 60 и выше | |||||
| Итого | - | - | - | - |
Необходимо рассчитать средний размер дохода на одного человека по всем группам семей и средний коэффициент эластичности.
Решение:
Средний размер дохода на одного человека по всем группам семей определим по формуле средней арифметической взвешенной:
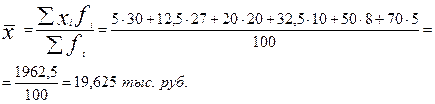
Для того чтобы исчислить средний коэффициент эластичности, необходимо определить коэффициенты эластичности в каждой группе.
Построим вспомогательную таблицу.
| Группы семей по доходу тыс. руб. | Средний размер дохода, тыс. руб.,
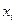
| Число семей,
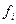
| Средний размер разовой покупки, тыс. руб.
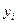
| Прирост доходов, тыс. руб.
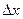
| Прирост размера покупки
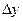
| Коэффициенты эластичности
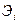
| Взвеш. коэф. эластичности
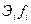
|
| До 10 | 0,5 | - | - | - | - | ||
| 10-15 | 12,5 | 0,7 | 7,5 | 0,2 | 0,267 | 7,209 | |
| 15-25 | 7,5 | 0,3 | 0,714 | 14,28 | |||
| 25-40 | 32,5 | 12,5 | 1,6 | ||||
| 40-60 | 17,5 | 1,857 | 14,856 | ||||
| 60 и выше | 1,875 | 9,375 | |||||
| Итого | - | - | - | - | - | 61,72 |
Средний коэффициент эластичности определим по формуле средней арифметической взвешенной:
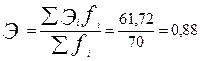
Задача 6. Данные о распределении населения по среднедушевому денежному доходу приведены в таблице:
| Все население | 100,0 |
| в том числе со среднедушевым денежным доходом, руб./мес.: | |
| До 5000 | 1,9 |
| 5000–10000 | 6,4 |
| 10000–15000 | 26,2 |
| 15000–20000 | 34,5 |
| 20000–25000 | 23,8 |
| 25000 и выше | 7,2 |
Определить:
1. среднедушевой месячный доход;
2. модальный и медианный доход;
3. нижний и верхний квартили;
4. нижний и верхний децили;
5. децильный коэффициент дифференциации доходов населения.
Решение:
Для расчета показателей составим вспомогательную таблицу:
| Среднедушевой денежный доход, руб./мес. | Численность
населения,
% к итогу
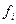
| Середина
интервала
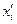
|
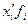
| Накопленная
частость численности населения
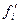
|
| До 5000 | 1,9 | 1,9 | ||
| 5000–10000 | 6,4 | 8,3 | ||
| 10000–15000 | 26,2 | 34,5 | ||
| 15000–20000 | 34,5 | 69,0 | ||
| 20000–25000 | 23,8 | 92,8 | ||
| 25000 и выше | 7,2 | |||
| Итого |
1. Среднедушевой денежный доход равен:
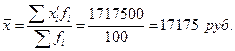
2. Модальный доход:
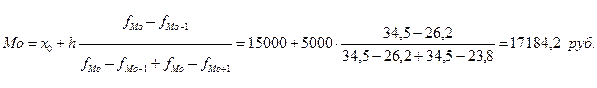 Таким образом, наиболее часто встречающийся доход населения 17184,2 рубля.
Таким образом, наиболее часто встречающийся доход населения 17184,2 рубля.
Медианный доход:
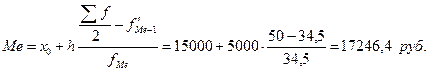
Следовательно 50% населения имеет доход меньше, чем 17246,4 рубля и 50% - больше, чем 17246,4 рубля.
3. Нижний квартиль:
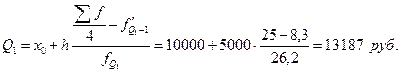
Следовательно, 25% населения имеет доход меньше, чем 13187 рублей, и 75% населения имеет доход больше, чем 13187 рублей.
Верхний квартиль:
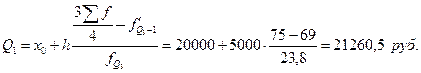
Следовательно, 75% населения имеет доход меньше, чем 21260,5 рублей, и 25% населения имеет доход больше, чем 21260,5 рублей.
4. Нижний дециль:
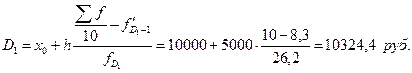
Верхний дециль:
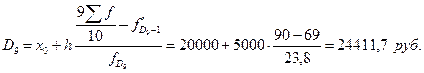
5. Децильный коэффициент дифференциации:
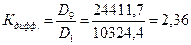 .
.
Таким образом, разница между доходами 10% самых богатых и 10% самых бедных слоев населения составляет 2,36 раз.
Дата добавления: 2016-01-26; просмотров: 31658;
