Решение типовых задач. Задача 1. Объем реализации говядины и цены в двух областях за 2 года представлены в таблице (данные условные): Регион 2001 год 2011 год
Задача 1. Объем реализации говядины и цены в двух областях за 2 года представлены в таблице (данные условные):
| Регион | 2001 год | 2011 год | ||
| Цена, руб./кг. | Количество, т. | Цена, руб./кг. | Количество, т. | |
| Область А | 72,3 | 236,6 | ||
| Область Б | 64,5 | 211,7 |
Определить:
1. индивидуальные индексы цен на говядину в каждой области;
2. среднюю цену на говядину за каждый период;
3. индексы средних цен переменного состава, постоянного состава и структурных сдвигов. Сделать выводы.
Решение:
1. Индивидуальный индекс цен на говядину по области А равен:
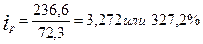 .
.
Индивидуальный индекс цен на говядину по области Б равен:
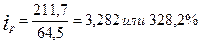 .
.
Среднюю цену на говядину по двум областям определим по формуле средней арифметической взвешенной:
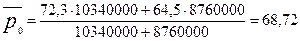 руб.
руб.
 руб.
руб.
Индекс переменного состава равен:
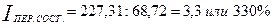
В абсолютном выражении: 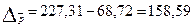 руб.
руб.
Индекс постоянного состава равен:
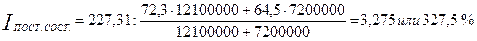
В абсолютном выражении: 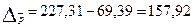 руб.
руб.
Индекс структурных сдвигов равен:
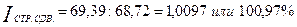
В абсолютном выражении: 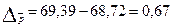 рубля.
рубля.
Таким образом, цена на говядину в двух областях повысилась в 2011 году по сравнению с 2001 годом более чем в 3 раза. В области А цена повысилась на 227%, в области Б – на 228 процентов. Изменение средней цены составило 3,3 раза или 158,59 руб., в том числе за счет изменения цен в каждой области средняя цена повысилась в 3,275 раза или на 157,92 руб., за счет структурных сдвигов средняя цена увеличилась на 0,97% (0,67 рубля).
Задача 2. Известны следующие данные о продаже товара за два года:
| Квартал | 2008 год | 2011 год | ||
| Цена, руб. | Кол-во проданных товаров, тыс. шт. | Цена, руб. | Выручка от продажи товаров, тыс. руб. | |
| Итого | - | - |
Выявить степень устойчивости цен посредством вариационного анализа (коэффициентов вариации). Сделать выводы.
Решение:
Определим средние цены в 2008 году и в 2011 году:
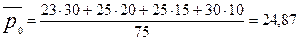 руб.
руб.
 руб.
руб.
Рассчитаем среднее квадратическое отклонение за каждый год:
в 2008 году:
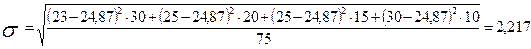 руб.
руб.
в 2011 году:
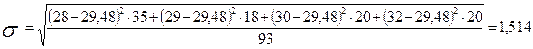 руб.
руб.
Коэффициент вариации в 2008 году равен:
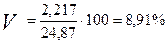
Коэффициент вариации в 2011году равен:
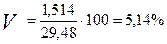
Значения коэффициентов вариации говорят о том, что цены устойчивы, не подвержены большим внутригодовым колебаниям.
Задача 3. На вторичном рынке жилья действуют средние цены (на начало года, руб. за 1 кв. м. общей площади жилья) за 2 года:
| Вид квартиры | 2010 год | 2011 год |
| 1-комнатная | 35 200 | 37 800 |
| 2-комнатная | 32 540 | 34 790 |
| 3-комнатная | 30 470 | 32 260 |
| 4-комнатная | 29 800 | 31 920 |
Определить: индивидуальные индексы цен и субиндексы Дюто, Карли, Джевонса.
Решение:
Для каждого вида квартир индивидуальные индексы цен равны:
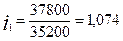 ,
,
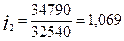 ,
,
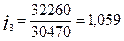 ,
,
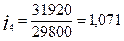 .
.
Индивидуальные индексы характеризуют изменение ценовой ситуации на рынке недвижимости следующим образом: цены за 1 кв. м. общей площади по всем видам жилья выросли. Наименьший рост цен определен на 3-комнатные квартиры. Он составил 105,9% (прирост – 5,9 процента). Больше всего выросли цены на однокомнатные квартиры – на 7,4 процента.
Определим индекс Дюто:
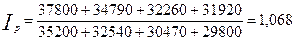 .
.
Таким образом, в среднем цена 1квадратного метра общей площади по всем видам квартир выросла на 6,8 процента.
Определим индекс Карли:
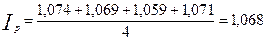
Определим индекс Джевонса:
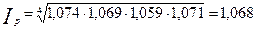
Индексы Карли и Джевонса также показали, что цена 1 квадратного метра выросла в среднем на 6,8 процента.
Задача 4. Индексы потребительских цен на непродовольственные товары в 2010 году представлены в таблице,% к декабрю 2009 года.:
| Июль | Август | Сентябрь | Октябрь | Ноябрь | Декабрь |
| 105,6 | 107,3 | 108,9 | 110,2 | 111,8 | 112,5 |
Рассчитать, как изменилась покупательная способность рубля за этот период времени.
Решение:
Чтобы определить индекс покупательной способности рубля, необходимо определить индекс цен. Так как известны базисные индексы цен к декабрю прошлого года, то искомый индекс цен за анализируемый период можно найти делением последнего индекса на первый:
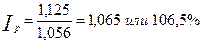
Следовательно, покупательная способность рубля равна:
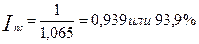
Покупательная способность рубля снизилась за рассматриваемый период на 6,1 процента.
Задача 5. Имеются следующие данные о ВВП и совокупной денежной массе по РФ:
| Показатели | Ед. изм. | 2009 год | 2011 год |
| Валовой внутренний продукт в текущих ценах | млрд. руб. | 38 807,2 | 54 585,6 |
| Валовой внутренний продукт в постоянных ценах (2008 года) | млрд. руб. | 38 048,6 | 41 421 |
| Денежная масса (в среднем за год) | млрд. руб. | 12 585,65 | 20 725,47 |
| Оборачиваемость денежной массы | обороты | 3,083 | 2,634 |
Определить индексы-дефляторы ВВП, а также абсолютное изменение денежной массы за счет изменения цен, физического объема ВВП и скорости обращения денежной массы, используя уравнение обмена Фишера.
Решение:
1. Определим индексы-дефляторы ВВП:
2009 год: 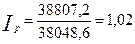 .
.
2011 год: 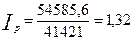 .
.
2. Как известно, взаимосвязь между индексами объемных и индексами качественных показателей аналогична взаимосвязи самих показателей.
Руководствуясь данным правилом, запишем уравнение обмена Фишера в динамике:
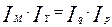 или
или 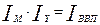 ,
,
где 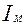 - индекс денежной массы,
- индекс денежной массы, 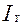 - индекс скорости обращения денежной массы,
- индекс скорости обращения денежной массы, 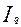 - индекс физического объема ВВП,
- индекс физического объема ВВП, 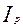 - индекс-дефлятор ВВП,
- индекс-дефлятор ВВП, 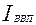 - индекс ВВП в текущих ценах.
- индекс ВВП в текущих ценах.
Из данной взаимосвязи индексов можно выразить абсолютное изменение показателей, т. е. провести факторный анализ.
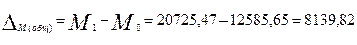 млрд руб. – абсолютное изменение денежной массы за счет всех факторов.
млрд руб. – абсолютное изменение денежной массы за счет всех факторов.
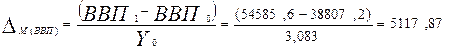 млрд руб. – абсолютное изменение денежной массы за счет динамики ВВП.
млрд руб. – абсолютное изменение денежной массы за счет динамики ВВП.
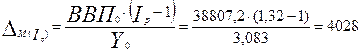 млрд руб. - абсолютное изменение денежной массы за счет изменения цен (индекса-дефлятора ВВП).
млрд руб. - абсолютное изменение денежной массы за счет изменения цен (индекса-дефлятора ВВП).
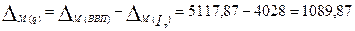 млрд руб. - абсолютное изменение денежной массы за счет физического объема ВВП.
млрд руб. - абсолютное изменение денежной массы за счет физического объема ВВП.
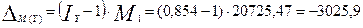 млрд руб. - абсолютное изменение денежной массы за счет изменения скорости обращения денежной массы.
млрд руб. - абсолютное изменение денежной массы за счет изменения скорости обращения денежной массы.
Дата добавления: 2016-01-26; просмотров: 2013;
