Глава 4. Статистика цен и инфляции

Статистическое изучение цен играет важную роль в анализе социально-экономических процессов как на уровне государства, так и на уровне хозяйствующих субъектов.

Статистика цен включает изучение следующих показателей:

1. Исчисление средних цен;

2. Показатели вариации цен;

3. Показатели динамики цен.

Средняя цена за единицу товара (услуги) – обобщенная характеристика цен товаров-представителей однородной товарной группы во времени и в пространстве.

Товар-представитель – совокупность определенных видов товаров в товарной группе, которые отличаются друг от друга незначительными особенностями, не влияющими на качество и потребительские свойства, однородны по назначению.

Существует несколько методических подходов к исчислению средних цен.

Средняя арифметическая простая используется в случаях, когда исходной информацией является уровень цен товара-представителя на начало и конец месяца. В таком случае применяется формула:

,

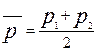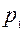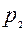где и - уровни цен на начало и конец месяца соответственно.

Если рассматриваются несколько разновидностей товаров-представителей, то средняя цена товара j исчисляется по средней арифметической или по средней геометрической:

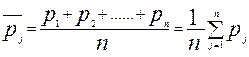
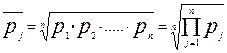
Средняя арифметическая взвешенная используется в случаях, если исходной информацией являются цены и количество реализованных товаров (или доли каждого товара в общем объеме товаров).

,

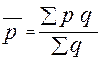где 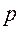- цена товара, 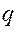- количество реализованных товаров или удельные веса отдельных товаров в общем количестве товаров.

Показатели вариации цен характеризуют степень их устойчивости, то есть отклонение уровня фактических цен от устойчивого уровня (средней цены) под влиянием колебаний спроса и предложения, различий в качестве товаров и технологии продажи, покупательной способности населения, региональных особенностей, а также случайных факторов.

Статистический анализ вариации цен проводится во времени и в пространстве.

Анализ вариации цен в экономическом пространстве может включать оценку ценовой однородности товарной группы, изучение колеблемости цен по регионам и городам, различным рынкам.

Анализ вариации цен во времени может включать оценку внутригодовых (сезонных) колебаний и циклических колебаний (например, по стадиям экономических или товарных циклов).

К показателям вариации цен относят: размах вариации цен, обобщающие показатели - среднее линейное отклонение цен, среднее квадратическое отклонение цен, коэффициент вариации цен.

Размах вариации цен находится как разница максимальной и минимальной цены:

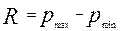
Среднее линейное отклонение цен определяется как простое и взвешенное по следующим формулам:

или ,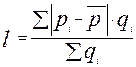

где 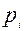- цена товара в i-й момент времени или в i-м пространстве, 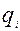- количество реализованного товара в i-й момент времени или в i-м пространстве, 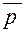- средняя цена за весь рассматриваемый период или на определенной территории (регион, город, рынок).

Среднее квадратическое отклонение находится по формулам:

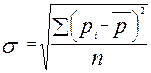или .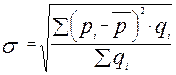

При условии массовой продажи допустимо заменить в этих формулах среднее значение цены на модальное.

Средние отклонения дают оценку в денежных единицах и не учитывают базу отклонения. Поэтому анализ дополняется расчетом коэффициента вариации, который измеряется в процентах:

.

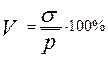Если 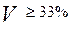, считается, что колебания цен значительны.

Коэффициент вариации предполагает, что для дорогих товаров допустим больший разброс индивидуальных значений цен. Недостаток коэффициента вариации состоит в том, что он позволяет определить колеблемость цены одного товара, а не совокупности разных товаров.

Анализ динамики цен включает определение индивидуальных, общих индексов цен, а также индексов средних цен переменного состава, постоянного состава и структурных сдвигов.

Индивидуальный индекс цен характеризует динамику цены отдельного товара или услуги и определяется по формулам:

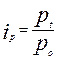(базисный индекс),

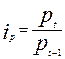(цепной индекс),

где 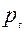- цена товара в текущем периоде t, 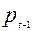- цена товара в предыдущем периоде, 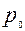- цена товара в базисном периоде.

Индивидуальный индекс цен по виду товара j исчисляется на основе информации об уровне цен или их изменении на товары-представители, его определяющие.

В международной статистике применяется несколько субиндексов для однородных групп товаров.

Индекс Ш. Дюто – характеризует отношение суммы цен товаров в отчетном периоде к сумме цен тех же товаров в базисном периоде. Рассчитывается по формуле:

.

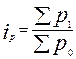Индекс Д. Карли – простое (невзвешенное) среднее арифметическое индивидуальных индексов цен или соотношений цен для двух сравниваемых периодов. Определяется по формуле:

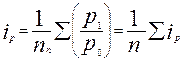
Индекс Юнга – взвешенное среднее арифметическое индивидуальных индексов цен или соотношений цен для двух сравниваемых периодов.

Средний геометрический индекс У. Джевонса – простое геометрическое индивидуальных индексов цен, что эквивалентно соотношению невзвешенных средних геометрических цен. Формула расчета имеет вид:

.

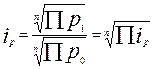Для разнородных видов товаров в статистике вычисляются агрегатные индексы.

Агрегатный индекс цен – это относительный показатель, который характеризует изменение цен не по отдельным товарам, а в среднем по совокупности товаров. В качестве весов используются физические объемы производства или реализации товаров (услуг).

Индекс цен Э. Ласпейреса – взвешенное по физическим объемам базисного периода, соотношение агрегированных цен. Формула расчета имеет вид:

,

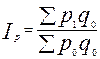где 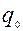- физический объем товара в базисном периоде, 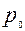и 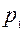- цена единицы товара соответственно в базисном и отчетном периодах.

Если из числителя индекса вычесть знаменатель, то можно определить абсолютное изменение (экономию или перерасход) в денежных единицах, которое можно было бы получить от изменения цен по той продукции, которая была произведена или реализована в базисном периоде:

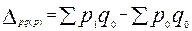
Индексу цен Ласпейреса соответствует средний арифметический индекс цен:

.

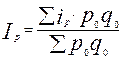Индекс цен Г. Пааше – сравнение агрегированных цен, взвешенных по физическим объемам текущего периода. Определяется по формуле:

.

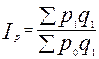Индекс показывает, во сколько раз изменился в среднем уровень цен по товарам, произведенным или реализованным в текущем периоде.

Если из числителя индекса вычесть знаменатель, то можно определить абсолютное изменение стоимости товаров (товарооборота) в текущем периоде по сравнению с базисным, за счет изменения цен.

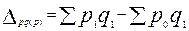
Индексу Пааше соответствует средний гармонический индекс цен:

.

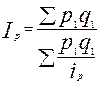Согласно теории индексов индекс по Ласпейресу искажает измерение “истинного” значения теоретического индекса цен в сторону завышения, тогда как индекс по Пааше - в сторону занижения, что называется “эффектом Гершенкрона”.

Для устранения этого эффекта теорией рекомендуется использование «идеального» индекса Фишера – средней геометрической из произведений агрегатных индексов Паше и Ласпейреса.

Формула имеет вид:

.

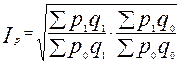Индекс цен Маршала – Эджворта – отражает изменение цен по условной структуре товаров, полученной на основе усреднения количества текущего и базисного периода. Формула расчета имеет вид:

.

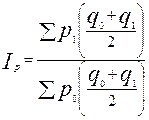Индекс Уолша - отражает изменение цен по условной структуре товаров, полученной на основе средней геометрической из произведений количества текущего и базисного периода. Индекс определяется по формуле:

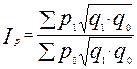
Индекс Торнквиста – среднее геометрическое соотношений цен, где в качестве весов используются средние значения долей стоимости двух сравниваемых периодов.

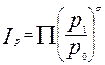, где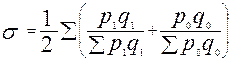

Для определения динамики средних цен используется система индексов: переменного состава, постоянного состава и структурных сдвигов.

Индекс средней цены переменного состава характеризует увеличение или уменьшение средней цены по группе товаров в результате влияния двух факторов (изменения цены каждого товара и структуры товаров).

Индекс переменного состава находится по формуле:

.

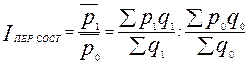Индекс средней цены постоянного состава характеризует увеличение или уменьшение средней цены по группе товаров в результате влияния одного фактора (изменения цены каждого товара).

Индекс постоянного состава находится по формуле:

.

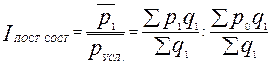Индекс средней цены структурных сдвигов характеризует увеличение или уменьшение средней цены по группе товаров в результате влияния одного фактора (структуры товаров).

Индекс структурных сдвигов находится по формуле:

.

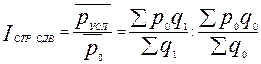Абсолютное изменение средней цены под влиянием отдельных факторов можно вычислить путем разности числителя и знаменателя каждого из вышеперечисленных индексов.