Методы исключения грубых погрешностей.

Грубая погрешность - это погрешность результата измерения, входящего в ряд измерений, которая «резко» отличается от остальных результатов. Они могут существенно исказить точечные оценки и доверительный интервал.

Промах невозможно обнаружить при однократном измерении. Для его уменьшения измерения проводит 3 - 5 раз, а за результат принимают среднее значение. При многократных измерениях используются статистические критерии.

В общем случае границы для промахов завися от объема выборки (СКО) и вида распределения т.е. 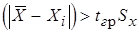. Коэффициент t_гр зависит от уровня значимости:

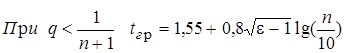, где e - эксцесс распределения.

Данное выражение используется при экспоненциальном, островершинном двухмодальном, Лапласа, равномерном, нормальном распределении с e = 1,5 - 6, для последнего e = 1,5 - 3

1. Правило трех сигм, используется для нормальных законов распределения и числа измерений 20 … 50. В этом случае считается, что результат, возникающий с вероятностью Р £ 0,003, не реален и его можно квалифицировать как промах. Сомнительный результат x_i отбрасывается если: 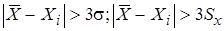.Затем среднее значение и СКО вычисляют заново.

2. Критерий Романовского, при n < 20. Вычисляется отношение 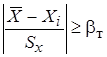которое сравнивается с табличным при выбранном уровне значимости, в зависимости от числа наблюдений, если расчетное значение больше табличного, то результат считается промахом.

3. Критерий Шовинэ, при n < 10. Результат считается промахом, если разность |Х_ср - Х_i| превышает значения S_x,:

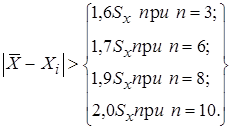
4. Критерий Шарлье, при n > 5 (5 … 100) 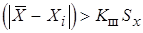. Значения критерия определяются по табл., случае выполнения неравенства результат отбрасывается.

5. Критерий Диксона при n = 4 … 30. Его особенность заключается в том, что результаты измерений раскладываются в вариационный возрастающий ряд. Х₁ … Х_n.

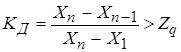Z_q - табл. значение, зависящее от уровня значимости, в случае выполнения неравенства результат отбрасывается.