Семейство распределений Стьюдента.

Описывает плотность распределения вероятностей среднего арифметического, вычисленного по выборке из n случайных отсчетов нормального распределения. Этот вид распределений используется при статистической обработке.

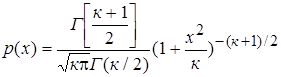
где к – число степеней свободы, зависящий от числа n: к = n-1. Общий вид распределения Стьюдента похож на распределение Гаусса. При больших к оно становится распределением Гаусса.

Особенность распределения: при числе измерений больше 3 СКО = ¥. Разновидностью этого распределения является распределение Коши - предельное распределение семейства законов Стьюдента с минимально возможным числом степеней свободы т.е. к=1.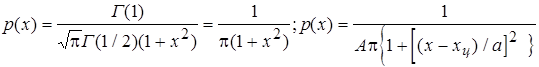

В общем виде распределение коши имеет вид: Свойства семейства Коши: - дисперсия и СКО не существуют, т.к. определяющий их интеграл расходится. Они будут бесконечно расти при росте числа экспериментальных данных. Оценка ширины распределения может быть произведена только на основе теории информации; - оценка в виде среднего арифметического неправомочна, т.к. ее рассеяние s/Ön =¥;- мат. ожидание не существует; - х_ц определяется через медиану; - энтропийное значение погрешности = 2pа.