Метод условных распределений
Метод основан на рекуррентном вычислении условных плотностей вероятностей для каждой из компонент случайного вектора X с многомерной совместной плотностью вероятности 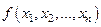 .
.
Для плотности распределения случайного вектора X можно записать:
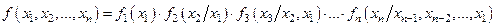 ,
,
где 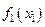 — плотность распределения СВ
— плотность распределения СВ 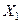 ;
; 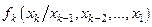 — плотность условного распределения СВ Xk при условии:
— плотность условного распределения СВ Xk при условии: 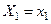 ;
; 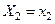 ; …;
; …; 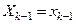 .
.
Для получения указанных плотностей необходимо провести интегрирование совместной плотности распределения случайного вектора в соответствующих пределах:
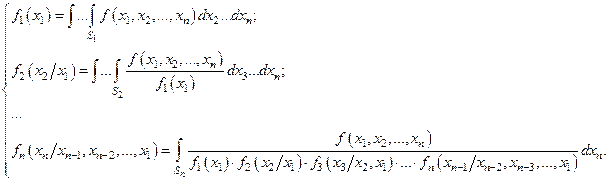
Порядок моделирования:
§ моделировать значение 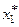 СВ
СВ 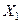 по закону
по закону 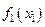 ;
;
§ моделировать значение 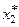 СВ
СВ 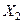 по закону
по закону  ;
;
§ ...;
§ моделировать значение 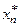 СВ
СВ 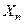 по закону
по закону 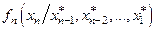 .
.
Тогда вектор 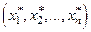 и есть реализация искомого случайного вектора X.
и есть реализация искомого случайного вектора X.
Метод условных распределений (как и метод обратной функции для скалярной СВ) позволяет учесть все статистические свойства случайного вектора. Поэтому справедлив вывод: если имеется возможность получить условные плотности распределения 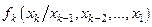 , следует пользоваться именно этим методом.
, следует пользоваться именно этим методом.
Метод исключения (Неймана)
Метод является обобщением уже рассмотренного для СВ метода Неймана на случай п переменных. Предполагается, что все компоненты случайного вектора распределены в конечных интервалах
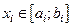 .
. 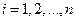 .
.
Если это не так, необходимо произвести усечение плотности распределения для выполнения данного условия.
Алгоритм метода:
1. Генерируются 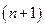 ПСЧ:
ПСЧ: 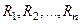 ;
; 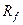 , распределенных, соответственно, на интервалах
, распределенных, соответственно, на интервалах 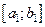 ,
, 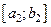 ,…,
,…, 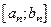 ;
; 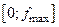 ;
;
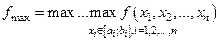 .
.
2. Если выполняется условие: 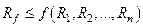 , то вектор
, то вектор 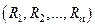 и есть искомая реализация случайного вектора.
и есть искомая реализация случайного вектора.
3. Если данное условие не выполняется, переходят к первому пункту и т.д.
Рис. 3 содержит иллюстрацию данного алгоритма для двумерного случая.
Возврат к п. 1 после "неудачного" моделирования п ПСЧ происходит тогда, когда точка Q окажется выше поверхности, представляющей двумерную плотность вероятности 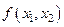 .Для случая, представленного на рисунке, в качестве (очередной) реализации двумерного случайного вектора следует взять пару ПСЧ
.Для случая, представленного на рисунке, в качестве (очередной) реализации двумерного случайного вектора следует взять пару ПСЧ 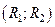 .
.
Среднюю относительную частоту "неудач" можно вычислить геометрическим способом, взяв отношение объемов соответствующих фигур.
Для одномерного случая, основным достоинством метода Неймана является его универсальность. Однако для плотностей вероятностей, поверхности которых имеют острые пики, достаточно часто будут встречаться "пустые" прогоны, когда очередные n ПСЧ бракуются. Этот недостаток тем существеннее, чем больше размерность моделируемого вектора 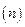 и длиннее требуемая выборка реализаций случайного вектора. На практике такие ситуации встречаются не слишком часто, поэтому метод исключений и имеет столь широкое распространение.
и длиннее требуемая выборка реализаций случайного вектора. На практике такие ситуации встречаются не слишком часто, поэтому метод исключений и имеет столь широкое распространение.
Рис. 3. Моделирование двумерного случайного вектора методом Неймана.
Дата добавления: 2016-01-11; просмотров: 1320;
