Метод обратной функции

Метод позволяет при моделировании СВ учесть все ее статистические свойства и основан на следующей теореме:

Если непрерывная СВ Y имеет плотность вероятности 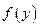, то СВ X, определяемая преобразованием

,

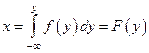имеет равномерный закон распределения на интервале [0;1].

Теорему доказывает следующая цепочка рассуждений, основанная на определении понятия "функция распределения" и условии теоремы:

.

Таким образом, получили равенство 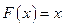, а это и означает, что СВ X распределена равномерно в интервале [0;1].

Напомним, что в общем виде функция распределения равномерно распределенной на интервале 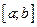СВ X имеет вид:

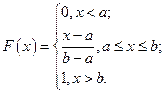
Теперь можно найти обратное преобразование функции распределения .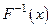

Если такое преобразование существует (условием этого является наличие первой производной у функции распределения), алгоритм метода включает всего два шага:

§ моделирование ПСЧ, равномерно распределенного на интервале [0;1];

§ подстановка этого ПСЧ в обратную функцию и вычисление значения СВ Y:

.

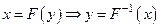При необходимости эти два шага повторяются столько раз, сколько возможных значений СВ Y требуется получить.

Простота метода обратной функции позволяет сформулировать такой вывод: если обратное преобразование функции распределения СВ, возможные значения которой необходимо получить, существует, следует использовать именно этот метод. К сожалению, круг СВ с функциями распределения, допускающими обратное преобразование, не столь широк, что потребовало разработки иных методов.

Метод исключения (Неймана)

Метод Неймана позволяет из совокупности равномерно распределенных ПСЧ 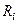, по определенным правилам выбрать совокупность значений с требуемой функцией распределения .

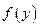Алгоритм метода

1. Выполняется усечение исходного распределения таким образом, чтобы область возможных значений СВ Y совпадала с интервалом .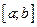

В результате формируется плотность вероятности 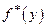такая, что

.

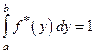Длина интервала 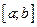определяется требуемой точностью моделирования значений СВ в рамках конкретного исследования.

2. Генерируется пара ПСЧ 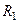и 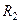, равномерно распределенных на интервале [0;1].

3. Вычисляется пара ПСЧ 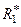и по формулам:

;

,

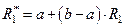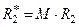где .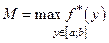

На координатной плоскости пара чисел 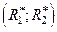определяет точку — например, точку на рис. 1. На рисунке обозначены: А— прямоугольник, ограничивающий график плотности распределения моделируемой СВ; D — область прямоугольника А, находящаяся ниже графика 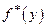; В — область прямоугольника А, находящаяся выше графика .

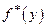4. Если точка 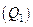принадлежит области D, считают, что получено первое требуемое значение СВ .

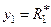5. Генерируется следующая пара ПСЧ 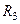и 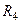равномерно распределенных на интервале [0;1], после пересчета по п. 3 задающих на координатной плоскости вторую точку — .

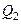6. Если точка 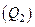принадлежит области В, переходят к моделированию следующей пары ПСЧ 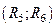и т.д. до получения необходимого количества ПСЧ.

Рис. 1.Моделирование СВ методом Неймана.

Очевидно, что в ряде случаев (при попадании изображающих точек в область В соответствующие ПСЧ с нечетными индексами не могут быть включены в требуемую выборку возможных значений моделируемой СВ, причем это будет происходить тем чаще, чем сильнее график 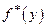по форме будет "отличаться" от прямоугольника А. Оценить среднее относительное число q "пустых" обращений к генератору ПСЧ можно геометрическим методом, вычислив отношение площадей соответствующих областей (В и А):

;

;

.

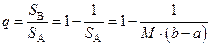Главным достоинством метода Неймана является его универсальность — применимость для генерации СВ, имеющих любую вычислимую или заданную таблично плотность вероятности.

Метод композиции

Применение метода основано на теоремах теории вероятностей, доказывающих представимость одной СВ композицией двух или более СВ, имеющих относительно простые, более легко реализуемые законы распределения. Наиболее часто данным методом пользуются для генерации ПСЧ, имеющих нормальное распределение. Согласно центральной предельной теореме распределение СВ Y, задаваемой преобразованием

,

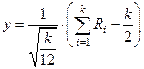где 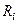— равномерно распределенные на интервале [0;1] ПСЧ, при росте k неограниченно приближается к нормальному распределению со стандартными параметрами .

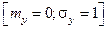Последнее обстоятельство легко подтверждается следующим образом. Введем СВ Z и найдем параметры ее распределения, используя соответствующие теоремы о математическом ожидании и дисперсии суммы СВ:

;

;

.

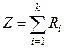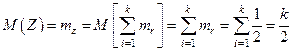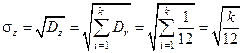Напомним, что при равномерном распределении в интервале [0;1] СВ имеет параметры:

; .

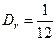Очевидно, что

,

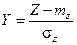и, как любая центрированно-нормированная СВ, имеет стандартные параметры.

Как правило, берут и считают, что для подавляющего числа практических задач обеспечивается должная точность вычислений. Если же к точности имитации предъявляются особые требования, можно улучшить качество моделирования СВ за счет введения нелинейной поправки:

,

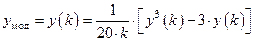где 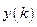— возможное значение СВ Y, полученное в результате сложения, центрирования и нормирования k равномерно распределенных ПСЧ .

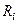В целом можно сделать вывод о том, что метод композиции применим и дает хорошие результаты тогда, когда из теории вероятностей известно, композиция каких легко моделируемых СВ позволяет получить СВ с требуемым законом распределения.