Метод линейных преобразований

Метод линейных преобразований является одним из наиболее распространенных так называемых корреляционных методов, применяемых в случаях, когда при моделировании непрерывного n-мерного случайного вектора достаточно обеспечить лишь требуемые значения элементов корреляционной матрицы этого вектора (это особенно важно для случая нормального распределения, для которого выполнение названного требования означает выполнение достаточного условия полного статистического соответствия теоретического и моделируемого распределений).

Идея метода заключается в линейном преобразовании случайного n-мерного вектора Y с независимыми (чаще всего — нормально распределенными) компонентами в случайный вектор X с требуемыми корреляционной матрицей и вектором математических ожиданий компонент.

Математическая постановка задачи выглядит следующим образом.

Дано:корреляционная матрица и математическое ожидание вектора X

;

.

Требуется:найти такую матрицу В, которая позволяла бы в результате преобразования

, (1)

где Y — n-мерный вектор с независимыми нормально распределенными компонентами со стандартными параметрами, получить вектор X с требуемыми характеристиками.

Будем искать матрицу 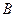в виде нижней треугольной матрицы, все элементы которой, расположенные выше главной диагонали, равны 0. Перейдем от матричной записи к системе алгебраических уравнений:

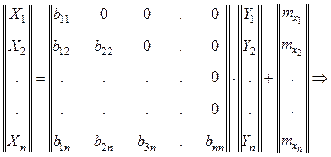
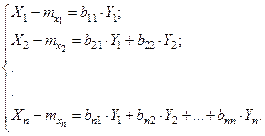(2)

Поскольку компоненты вектора Y независимы и имеют стандартные параметры, справедливо выражение:

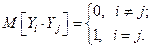
Почленно перемножив сами на себя и между собой соответственно левые и правые части уравнений системы (2) и взяв от результатов перемножения математическое ожидание, получим систему уравнений вида:

Как легко увидеть, в левых частях полученной системы уравнений — элементы заданной корреляционной матрицы Q а в правых — элементы искомой матрицы .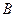

Последовательно решая эту систему, получаем формулы для расчета элементов :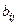

; ; ;…

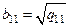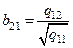Формула для расчета любого элемента матрицы преобразования 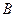имеет вид:

.

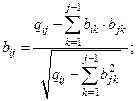
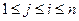Таким образом, алгоритм метода линейных преобразований весьма прост:

§ по заданной корреляционной матрице рассчитывают значения коэффициентов матрицы преобразования В;

§ генерируют, одну реализацию вектораY, компоненты которого независимы и распределены нормально со стандартными параметрами;

§ полученный вектор подставляют в выражение (1) и определяют очередную реализацию вектора X, имеющего заданные корреляционную матрицу и вектор математических ожиданий компонент;

§ при необходимости два предыдущих шага алгоритма повторяют требуемое число раз (до получения нужного количества реализаций вектора X).

Как правило, все современные программные средства, применяемые для реализации тех или иных имитационных моделей, содержат встроенные генераторы равномерно распределенных ПСЧ, что позволяет исследователю легко моделировать любые случайные факторы.

Лекция №15

Содержание лекции

Имитационные модели информационных систем... 1

Основы организации имитационного моделирования. 1

Этапы имитационного моделирования. 1

Испытание имитационной модели. 2

Задание исходной информации. 3

Верификация имитационной модели. 3

Проверка адекватности модели. 3

Калибровка имитационной модели. 4

Исследование свойств имитационной модели. 4

Оценка погрешности имитации, связанной с использованием в модели генераторов псевдослучайных чисел (ПСЧ) 4

Определение длительности переходного режима. 5

Оценка устойчивости результатов имитации. 6

Исследование чувствительности модели. 6

Языки моделирования. 7