Пример 1.4. «Статистические модели оценки кредитоспособности заемщиков».
Предположим, что за некоторый прошлый период доступны данные по группе компаний, включающей как компании, которые стали банкротами, так и компании, которые избежали краха[22]. Для простоты допустим, что будут проанализированы только два показателя: коэффициент текущей ликвидности (Ктл) и доля заемного капитала (Зк). Дискриминантная функция примет следующий вид:
Z = a + b×Ктл+ c×Зк. (1.5)
Параметры a, b и c дискриминантной функции рассчитываются в результате статистической обработки данных по выборке компаний, которые либо обанкротились, либо сумели выжить в течение некоторого периода. Так, по данным табл. 2.7, с помощью компьютерной программы дискриминантного анализа можно получить следующую зависимость:
Z = -0,3877 – 1,0736×Ктл + 0,0579×Зк (1.6)
Таблица 1.8
Расчет вероятности банкротства компаний
| Компания | Ктл | Зк, % | Факт банкротства | Индекс Z | Вероятность банкротства, % |
| 3,6 | Нет | -0,780 | 17,2 | ||
| 2 (А) | 3,0 | Нет | -2,451 | 0,8 | |
| 3,0 | Нет | -0.135 | 42,0 | ||
| 3,0 | Да | 0,791 | 81,2 | ||
| 2,8 | Нет | -0,847 | 15,5 | ||
| 2,6 | Да | 0,062 | 51,5 | ||
| 2,6 | Да | 0,757 | 80,2 | ||
| 2,4 | Да | -0,649 | 21,1 | ||
| 2,4 | Нет | 0,509 | 71,5 | ||
| 2,2 | Нет | -1,129 | 9.6 | ||
| 2,0 | Нет | -0,220 | 38,1 | ||
| 2,0 | Нет | 0,244 | 60,1 | ||
| 1,8 | Да | 1,153 | 89,7 | ||
| 1,6 | Нет | -0,948 | 13,1 | ||
| 1,6 | Да | 0,441 | 68,8 | ||
| 1,2 | Да | 0,871 | 83,5 | ||
| 1,0 | Нет | -0,072 | 45,0 | ||
| 1,0 | Да | 0,391 | 66,7 | ||
| 19 (В) | 1,0 | Да | 2,012 | 97,9 |
Эта функция Z изображена на рис. 1.3 как геометрическое место точек, для которых Z = 0.

Рис. 1.3. Графическая интерпретация вероятностей банкротства (LPB – малая вероятность банкротства; HPB – высокая вероятность банкротства; + компания выжила; – компания обанкротилась).
Компаниям, расположенным выше линии (то есть, имеющим Z<0), банкротство, вероятно, не грозит, тогда как компании, расположенные ниже линии (то есть, имеющие Z>0), могут в будущем разориться. На рис. 1.3 можно увидеть, что наблюдается только три отклонения от сформированной зависимости, когда местоположение точки не соответствует сделанным выводам. Тем не менее, вероятность получения правильного прогноза достаточно велика – 85%.
Чем выше значение Z, тем хуже выглядят компании с позиции возможного банкротства. Можно дать следующую интерпретацию индекса Z:
Z=0. Вероятность наступления банкротства в будущем (скажем, в течение двух лет) 50%. Значения Z таких компаний расположены прямо на линии разграничения.
Z<0. Вероятность наступления банкротства меньше 50%. Чем меньше Z, тем благоприятнее текущее финансовое положение.
Z>0. Вероятность наступления банкротства больше, чем 50%, и с ростом Z она увеличивается.
Знаки параметров дискриминантной функции имеют определенный смысл. Чем больше коэффициент текущей ликвидности (Ктл), тем меньше Z этой компании, то есть ниже вероятность банкротства. Подобным образом высокая доля заемного капитала (Зк) приводит к высокому значению Z, и это прямо отражается на увеличении вероятности банкротства.

S – устойчивое финансовое состояние ; UZ – “зона неведения”; B – банкротство.
Рис. 1.4. Распределение вероятностей значений индекса Z.
Среднее Z для компаний, которым не грозит банкротство, равно –0,583, а для потенциальных банкротов значение Z составляет +0,648. Можно интерпретировать рис. 1.4. следующим образом: если Z<-0,3, вероятность того, что компания будет двигаться к банкротству, очень мала, тогда как, если Z>0,3, существует небольшая вероятность того, что она останется платежеспособной. Если –0,3<Z<+0,3 (зона неведения), то определенного мнения о компании высказать нельзя.
Наша дискриминантная функция имеет только две переменные, но можно ввести и другие характеристики, например, рентабельность активов, оборачиваемость дебиторской задолженности, коэффициент быстрой ликвидности. При введении в рассмотрение нового параметра, например, показателя рентабельности активов (ROA), следует рассматривать новую дискриминантную функцию:
Z = a + b×Ктл+c×Зк + d×ROA. (1.7)
Не исключено, что по новому уравнению прогноз в отношении некоторых компаний изменится, то есть вполне вероятно, что добавление других характеристик заемщика улучшает точность прогнозирования банкротства. Другими словами, это приведет к тому, что распределение вероятностей становится более плотным, сужается зона неведения, и появляется возможность точнее классифицировать ту или иную компанию, то есть вероятность ошибки уменьшается.
Наиболее распространенными моделями MDA являются модели Альтмана и Чессера.
Модель Альтмана
«Z-анализ» был введен Альтманом, Хальдерманом и Нарайаной (1977 г.) и представлял собой модель выявления риска банкротства корпораций. Цель «Z-анализа» - отнести изучаемый объект к одной из двух групп: либо к фирмам-банкротам, либо к успешно действующим фирмам. Линейная модель Альтмана, или уравнение Z-оценки, выглядит следующим образом:
Z=1,2×Х1+1,4×Х2+3,3×Х3+1,0×Х5 (1.8)
где Х1 – отношение собственных оборотных средств к сумме активов;
Х2 – отношение нераспределенной прибыли к сумме активов;
Х3 – отношение брутто-прибыли (прибыли до вычета процентов и налогов) к сумме активов;
Х4 – отношение рыночной стоимости обыкновенных и привилегированных акций к балансовой оценке заемного капитала;
Х5 – отношение объема продаж (выручки от реализации) к сумме активов.
Модель Альтмана предсказывает случай наступления банкротства достаточно хорошо на два года вперед. Более поздние работы Альтмана и его коллег обновили и улучшили его первоначальное исследование - они применили прием сглаживания данных, чтобы выровнять случайные колебания. Новая модель способна предсказывать банкротства с высокой степенью точности на два года вперед и с меньшей, но все же приемлемой точностью (70%), на пять лет вперед[23].
Модель Чессера
Модель надзора за ссудами Чессера прогнозирует уже не факт банкротства компании, а случаи невыполнения заемщиком условий кредитного договора. При этом под «невыполнением условий» подразумевается не только полное непогашение ссуды, но и любые другие частичные отклонения от первоначальных условий, делающие ссуду менее выгодной для кредитора.
В модель Чессера входят следующие шесть параметров:
Х1 – отношение кассовой наличности и легко реализуемых ценных бумаг к сумме активов;
Х2 – отношение чистой суммы продаж (без учета НДС) к сумме кассовой наличности и легко реализуемым ценным бумагам активов;
Х3 – отношение брутто-дохода (прибыли до вычета процентов и налогов) к сумме активов;
Х4 – отношение совокупной задолженности к сумме активов;
Х5 – отношение основного капитала к чистым активам (или инвестируемому капиталу = акционерный капитал и долгосрочные кредиты);
Х6 – отношение оборотного капитала к нетто-продажам (чистой сумме продаж).
Оценочные показатели модели следующие:
Y = -2,0434-5,24×Х1+0,0053×Х2-6,6507×Х3+4,4009×Х4-0,0791×Х5-0,1020×Х6 (1.9)
Переменная Y, которая представляет собой линейную комбинацию независимых переменных, используется в следующей формуле для оценки вероятности невыполнения условий договора, Z:
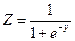 (1.10)
(1.10)
где e = 2,71828 (число Эйлера – основание натуральных логарифмов).
Получаемая оценка Y может рассматриваться как показатель вероятности невыполнения условий кредитного договора. Чем больше значение Y, тем выше вероятность невыполнения условий кредитного договора для данного заемщика. В модели Чессера для оценки вероятности невыполнения условий кредитного договора используются следующие условия:
если Z>0,50, то заемщика следует отнести к группе заемщиков, которые не выполнят условий договора;
если Z<0,50, то заемщика можно отнести к группе надежных заемщиков.
Чессер использовал данные ряда банков по 37 «удовлетворительным» ссудам и 37 «неудовлетворительным», причем для расчета были взяты показатели финансовой отчетности компаний за год до получения кредита. Подставив расчетные показатели в формулу «вероятности нарушения условий договора», Чессер правильно определил три из каждых четырех исследуемых случаев[24].
Используя математические методы при управлении кредитами банков, необходимо иметь в виду, что предоставление коммерческих кредитов не чисто технический процесс. Напротив, это сложный творческий процесс, в котором важны как субъективные отношения между сторонами, так и понимание математических закономерностей. Математические модели не учитывают роль межличностных отношений, а в практике кредитования этот фактор играет существенное значение при принятии решения о выдаче кредита.
Альтман предлагал использовать его «количественную модель» как дополнение к «качественному и интуитивному» подходу инспекторов кредитных отделов банков, отмечая, что его модель не дает рейтинговой оценки кредита и не способна заменить оценки, которые предлагают служащие банка. Такая модель и получаемые через нее Z-оценки могут послужить ценным инструментом определения общей кредитоспособности клиентов и сигналом раннего предупреждения о возможности ухудшения финансового состояния клиента.
Недостатками статистических моделейявляются:
• «количественная субрелевантность» (переоценка роли количественных факторов);
• произвольность выбора системы количественных показателей (финансовых коэффициентов),
• высокая чувствительность к недостоверности исходных данных (финансовой отчетности), что наиболее характерно для российских предприятий;
• громоздкость и сложность вычислений, необходимость использования математического аппарата;
• необходимость создания и поддержания статистической базы данных о заемщиках.
Дата добавления: 2016-01-26; просмотров: 1458;
