Понятие блочных и поточных шифров
Отправной точкой в реализации рассматриваемого подхода является идея вырабатывать гамму для зашифрования сообщения из самого сообщения. Однако сделать это непосредственно невозможно, так как при этом возникают трудности с расшифрованием: пусть гамма вырабатывается из шифруемого блока согласно уравнению Г=f(Т), где f -некоторая функция. При этом уравнение зашифрования будет иметь следующий вид: Т' = Ек(Т) = Т°Г=Т°f(Т). Для расшифрования сообщения его получатель должен решить это уравнение относительно T: T°f(T) = T'. Если функция f сложна и нелинейна, что требуется для обеспечения достаточной стойкости шифра, данная задача практически неразрешима.
Тем не менее, при разработке новой криптографической схемы не хотелось бы отказываться от ранее использованных и хорошо зарекомендовавших себя решений, к числу которых относится наложение гаммы на данные для их шифрования. Как же выйти из того затруднительного положения? Попытаемся решить хотя бы часть проблемы, для чего представим шифруемый блок данных T размера T=N в виде пары блоков меньшего размера: Т=(Т0,Т1), |T0| = N0, |T1| = N1, N0 + N1=N, где T0 будет обозначать младшую, а Т1 - старшую часть массива T. Выполним зашифрование старшего блока с помощью младшего, используя при этом некоторую функцию f, отображающую N1-битовый блок данных на N0-битовый, и обратимую бинарную операцию "°" над Побитовыми блоками данных. Полученное шифрующее преобразование обозначим через 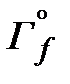 . Уравнение этого преобразования будет следующим:
. Уравнение этого преобразования будет следующим:
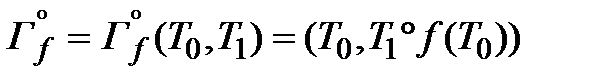
Для 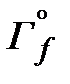 легко построить обратное, или расшифровывающее преобразование
легко построить обратное, или расшифровывающее преобразование 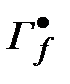 :
:
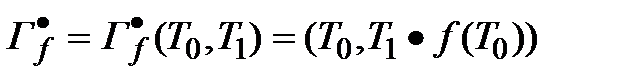
Действительно, если бинарные операции " ° " и " • " взаимно обратные, каков бы ни был N-битовый блок данных T= (T0,T1), всегда справедливо следующее равенство:
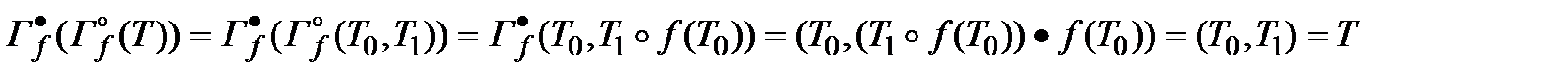
Ясно, что назначение функции f заключается в том, чтобы маскировать зависимость между блоком T0 и гаммой для шифрования блока T1, которая из него вырабатывается. Для этого функция f должна быть секретным элементом нашего шифра. Отметим очень важный факт: эта схема работоспособна при любой функции после расшифрования мы всегда получим те же самые данные, которые были перед зашифрованием.
Поточные шифры характерны тем, что шифруют информацию по одному биту за такт шифрования. Учитывая, что среди операций с битами существуют только две обратимые – сумма по модулю 2 и логическое отрицание, то выбор принципа шифрования очевиден – биты открытого текста должны складываться с битами ключевой последовательности с помощью операции Å:
ci = mi Å ki.
Дешифрование происходит аналогичным образом:
mi = ci Å ki.
Учитывая свойства операции сложения по модулю 2, можно отметить, что выполняется:
ki = ci Å mi,
поэтому криптостойкость поточных шифров полностью зависит от качества генератора потока ключей. Очевидно, что если поток ключей будет включать в себя только двоичные нули, то шифротекст будет представлять собой точную копию открытого текста. Поток ключей поточных шифров принято обозначать греческой буквой g (гамма), вследствие чего подобные шифры получили название шифров гаммирования. Большинство современных генераторов гаммы построено на линейных регистрах сдвига (ЛРС). Он представляет собой (рис.21.1) последовательность бит, которая на каждом такте шифрования сдвигается вправо на 1 разряд, при этом выход из крайнего правого бита является выходом генератора, а на вход крайнего левого бита подается значение, вычисляемое как сумма по модулю 2 нескольких разрядов ЛРС. Ключ шифрования поточного шифра заносится в ЛРС перед началом генерации гаммы.
| … |
| g |
| Рис.21.1 Линейный регистр сдвига |
| g |
| Рис.21.2 Линейный регистр сдвига на три разряда |
Занесем в регистр начальное значение 010 и посмотрим, какие значение получим на выходе гаммы.
Таблица 21.1
Результат работы генератора гаммы на основе ЛРС
| Номер такта | Значения битов ЛРС | Бит гаммы | ||
| нач.сост | - | |||
Из таблицы видно, что состояние ЛРС повторяется через 7 тактов (начальное состояние ЛРС совпадает с его состоянием на 7-м такте). Повтор состояния ЛРС означает, что и гамма будет периодически повторяться. Повторение гаммы снижает криптостойкость поточных шифров, позволяя криптоаналитику проводить анализ шифротекстов, полученных кодированием на одной и той же гамме. Поэтому при проектировании структуры ЛРС встает проблема достижения максимального периода повтора ЛРС. Для ЛРС длиной n бит максимальный период составляет 2n-1 тактов (состояние, когда все биты равны нулю, недопустимо, поскольку ЛРС любой структуры не выходит из этого состояния, зацикливаясь в нем). Построение ЛРС оптимальной структуры с точки зрения периода повторения гаммы имеет четкую математическую основу в виде теории неприводимых полиномов. Структура ЛРС описывается многочленом вида:
b1*xn+b2*xn-1+b3*xn-2+…+bn-1*x2+ bn*x+1,
где bi=0, если i-й бит слева не участвует в обратной связи, и bi=1, если участвует. ЛРС будет иметь максимально возможный период повторения гаммы, если описывающий его многочлен не раскладывается на произведение многочленов меньшей степени.
Основной проблемой ЛРС является их нестойкость к атаке на основе известного открытого текста. Даже если неизвестна внутренняя структура ЛРС, криптоаналитик с помощью алгоритма Берлекэмпа-Мэсси по известным 2N битам открытого текста и соответствующего шифротекста имеет возможность построить ЛРС, порождающую подобную последовательность. Поэтому современные поточные шифры строятся на основе нелинейных регистров сдвига (НРС). Нелинейные регистры сдвига строятся на основе линейных с добавлением в структуру нелинейных элементов: логического сложения и логического умножения. Наиболее популярными классами нелинейных регистров сдвига на сегодня являются фильтрующие, комбинирующие и динамические поточные шифры.
Фильтрующие НРС строятся с использованием дополнительной комбинационной схемы – фильтра – на выходах некоторых бит ЛРС (рис.21.4). Выход комбинационной схемы и является гаммой.
| ЛРС |
| … |
| КС |
| g |
| Рис.21.3. Поточный шифр на основе фильтрующего НРС |
Комбинирующие НРС также используют комбинационную схему с нелинейными преобразованиями бит, но на вход этой комбинационной схемы подаются выходы нескольких ЛРС (рис.2.12).
| ЛРС1 |
| ЛРС2 |
| ЛРСN |
| … |
| KC |
| g |
| Рис.21.4.. Поточный шифр на основе комбинирующего НРС |
При проектировании НРС комбинирующего типа необходимо следить, чтобы комбинационная схема равномерно перемешивала выходы каждого из ЛРС, иначе может возникнуть ситуация доминирования одного из ЛРС, когда его выход на подавляющем большинстве тактов совпадает с общим выходом НРС.
Динамические НРС также строятся на основе нескольких ЛРС, но здесь они вступают друг с другом в отношения «главный-подчиненный» (рис.21.5). В зависимости от выхода управляющего ЛРС на общий выход НРС подается либо выход первого, либо второго ЛРС.
В качестве примера поточного шифра, построенного на основе регистров сдвига, можно привести алгоритм A5, используемый для кодирования в стандарте GSM. A5 включает 3 ЛРС длиной 19, 22 и 23 бита на выход гаммы подается сумма по модулю 2 выходов всех регистров. Используется схема динамического НРС, когда каждый регистр тактируется в зависимости от состояния средних разрядов всех трех регистров сдвига.
Дата добавления: 2016-01-26; просмотров: 724;
