Основные прочностные характеристики

Прочность и жесткость являются важнейшими характеристиками любого материала. При нагружении образца растяжением или сжатием в нем возникают нормальные напряжения σ и соответствующие им деформации ε, которые растут вплоть до разрушения материала. Предельное (максимальное) напряжение называют его прочностью. Связь между упругими напряжениями σ, действующими на тело, и деформациями ε, вызванными этими напряжениями, устанавливает закон Гука. Для одностороннего растяжения или сжатия изотропного тела, на которое действует только одна сила, закон Гука записывается в виде

σ = Е∙ε . (2)

Коэффициент пропорциональности Е называют модулем упругости, или модулем нормальной упругости, или модулем Юнга.

Оценки упругих характеристик КМ основываются на допущениях о жесткой связи между матрицей и волокнами, их совместной деформации и подчинении закону Гука [6].

Для простейшей модели КМ – системы жестко свя­занных и чередующихся изотропных стержней, обладаю­щих характеристиками волокна, и матрицы – продольный модуль упругости Е_х (в направлении, продольном оси во­локон) рассчитывается по уравнению аддитивности, или правилу смесей:

E_x = E_в ∙V_в + E_м ∙V_м = E_в ∙V_в + E_м ∙ (1 – V_м), (3)

где E_в – модуль упругости волокон;

E_м – модуль упругости матрицы;

V_в – объемная доля волокон;

V_в – объемная доля матрицы.

Поперечный модуль упругости E_v (в направлении, перпендикулярном оси волокон) определяется из выраже­ния

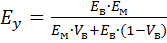. (4)

По аналогии с растяжением связь между касательны­ми напряжениями τ и соответствующими упругими сдви­говыми деформациями γ можно записать в виде выраже­ния:

τ = G∙γ . (5)

где G – модуль упругости при сдвиге (модуль сдвига).

В однонаправленном КМ при совпадении оси х с на­правлением укладки волокон модули G_xv и G_xz характери­зуют упругие сдвиги КМ в двух плоскостях ху и xz, парал­лельных волокнам. Правило аддитивности для КМ со сплошными волокнами можно представить следующим образом:

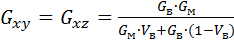. (6)

где 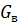– модуль сдвига волокон;

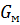– модуль сдвига матрицы.

При одноосном растяжении изотропного материала наряду с увеличением его длины в направлении действия силы (например, по оси х) уменьшаются поперечные раз­меры вдоль двух других осей (у и х). Отношение относи­тельных деформаций тела в поперечном ε_y и продольном ε_х направлениях называют коэффициентом Пуассона μ:

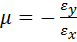. (7)

Величина μ_xy однонаправленного двухкомпонентного КМ по правилу смесей оценивается следующим образом:

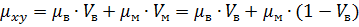, (8)

где 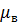– коэффициент Пуассона волокон;

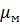– коэффициент Пуассона матрицы.

Следует отметить, что приведенные соотношения можно рассматривать только как приближенные, оценоч­ные, поскольку модели расчета идеализированы. Технологические дефекты, неоднородность распределения волокон по объему КМ, разориентация и неоднородность свойств компонентов приводят к тому, что реальные характеристи­ки армированных композиций отличаются от расчетных. Поэтому для паспортизации КМ обычно используют экс­периментально определенные упругие константы.

Упругие свойства изотропных материалов хорошо описываются двумя констан­тами Е и G, взаимосвязь между которыми соответствует уравнению

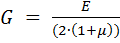. (9)

Приведенные соотношения хорошо описывают изотропные материалы, свойства которых во всех направлениях одинаковы. К таковым можно отнести дисперсно-наполненные полимеры, а также КМ на основе коротких или непрерыв­ных волокон хаотичной структуры. Для волокнистых материалов всегда имеется определенная степень ориентации, определенная влиянием технологических фак­торов.

При нагружении какой-либо конструкции напряженно-деформированное состояние материала чаше всего становится неоднородным. При этом предоставляется возможность выявить главные (максимальные) напряжения, которые могут явиться причиной ее разрушения. Например, в случае трубы, находящейся под внутренним или внешним давлением, окружные напряжения в два раза превосходят осевые напряжения, то есть половина толщины изотропного материала с точки зрения осевых напряжений неэффективна. Неоднородность поля напряжений может быть и существенно выше. Для оболочек с открытым выходом (ружья, стволы гранатометов) соотношение радиальных и осевых напряжений достигает от 8 до 10 и более. В этих случаях следует воспользоваться замечательной способностью волокнистых материалов, которые можно ориентировать в матрице в соответствии с распределением главных эксплуатационных напряжений [7].

5 Определение упругих характеристик однонаправленного слоя

Изучение механического поведения композиционных материалов проводится на двух уровнях абстрагирования. Первый уровень, называемый микромеханикой, включает тонкие детали структуры композита на уровне размеров волокна, которое помещено в матрицу. Основным результатом решения задачи в микромеханической постановке является вычисление эффективных модулей однонаправленного слоя, которые определяются как коэффициенты, связывающие усредненные по объему значения напряжений (компонент тензора напряжений) и деформаций (компонент тензора деформаций) при определенных граничных условиях.

Вычисление эффективных модулей композиционных материалов основано на понятии представительного элемента объема, то есть такого элемента, в котором все усредненные по объему компоненты напряжений и деформаций равны соответствующим величинам, вычисленным для рассматриваемого композита в целом. Как правило, микромеханика ограничивается вычислением эффективных модулей упругости и коэффициентов Пуассона однонаправленного композиционного слоя. Эти вычисления дают возможность дальнейшего аналитического исследования на новом уровне абстрагирования, а именно на уровне слоистого тела. При этом реальный неоднородный материал рассматривается как однородное анизотропное тело, состоящее из однонаправленных слоев, ориентированных под разными углами (рисунок 5).

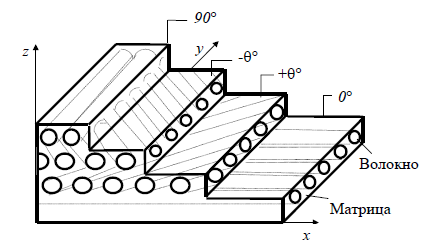
Рисунок 5 – Волокнистый композиционный материал с укладкой
слоев: 90°, -θ, θ, 0°

Слой – основной элемент в КМ, состоящий из погруженных в матрицу однонаправленных волокон. Следовательно, можно связать упругие и прочностные свойства однонаправленного слоя с соответствующими свойствами компонентов. Таким образом, имеется возможность проектировать элементы конструкций из волокнистых КМ, зная конструктивные требования к конструкции и свойства компонентов КМ.

При определении упругих постоянных однонаправленного слоя по известным упругим характеристикам волокон и связующего необходимо рассмотреть напряженно-деформированное состояние последних при нагружении слоя вдоль армирования, поперек и при сдвиге. Совместная работа волокна и связующего, обладающих различными упругими характеристиками, представляет собой сложную математическую задачу. Для определения напряжений и деформаций в компонентах КМ используют физические и математические модели как самих компонентов, так и модели их совместной работы.

Для упрощения расчетов вводится ряд допущений:

1) компоненты композиционного материала являются однородными и линейно-упругими материалами;

2) связующее является изотропным, а волокна могут быть изотропными или трансверсально-изотропными;

3) армирующие волокна являются прямыми и параллельными;

4) армирующие волокна распределены равномерно и имеют одинаковое сечение.

Сама модель их совместной работы предполагает, что между арматурой и связующим существует жесткое сцепление, то есть отсутствует скольжение. Поры как в арматуре и связующем, так и на поверхности их раздела отсутствуют.

Для определения напряжений в компонентах однонаправленного слоя в качестве расчетной модели будем пользоваться повторяющимся элементом структуры материала. Периодически повторяющийся элемент представляет собой типичную модель, применяемую в микромеханике для определения механических свойств КМ. На рисунке 6 показаны модели, которые используются для определения упругих свойств композитов на основе методов сопротивления материалов.

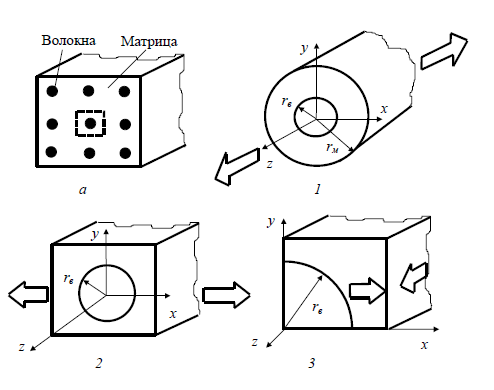
Рисунок 6 – Представительный объем композиционного материала (a) и
повторяющиеся элементы однонаправленного слоя для определения
продольного модуля упругости (1), поперечного модуля упругости (2) и
модуля сдвига (3)

В этой модели выделяются три элемента: первый – для определения поля внутренних напряжений при нагружении вдоль волокон, второй – для определения напряжений при нагружении поперек волокон, третий – для определения напряжений при сдвиге. Определение поля внутренних напряжений в волокне и связующем при различных видах нагружения представляет большие математические трудности. В инженерных расчетах, как правило, используют упрощенные модели, базирующиеся на методах сопротивления материалов.

В качестве упрощенной модели используется однонаправ­ленный слой, состоящий из объема, занятого армирующими волок­нами, и объема, занятого матрицей (рисунок 7).

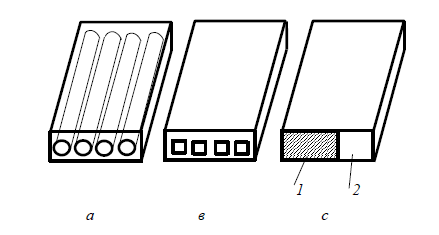
1 – объем, занятый волокном; 2 – объем, занятый матрицей

Рисунок 7 – Модели однонаправленного слоя с круглыми (а) и эквивалентными им по площади прямоугольными волокнами (в), с – упрощенная модель однонаправленного слоя для определения упругих свойств

Возможность в этой модели пренебречь влиянием коэффициентов Пуассона волокна и матрицы, геометрической формой поперечного сечения армирующих волокон при определении эффективных модулей упругости однонаправленного слоя позволяет существенно упростить расчеты [8].