Расчет упругих характеристик однонаправленного слоя
К упругим характеристикам однонаправленного слоя относят: продольный модуль упругости Е1, поперечный модуль Е2, модуль сдвига G12, коэффициент Пуассона υ12 и υ21.
Исходные данные для расчета приведены в таблицах 1, 2 и 3.
Таблица 1 – Механические характеристики бороволокна
Модуль упругости  , ГПа , ГПа
| |
| Модуль сдвига G12б, ГПа | |
Коэффициент Пуассона 
| 0,10 |
Предельное удлинение при растяжении  , % , %
|
Таблица 2 – Механические характеристики стекловолокна
Модуль упругости  , ГПа , ГПа
| |
| Модуль сдвига Gс, ГПа | |
Коэффициент Пуассона 
| 0,22 |
Предельное удлинение при растяжении  , % , %
|
Таблица 3 – Механические характеристики полиимидной матрицы
Модуль упругости 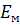 , ГПа , ГПа
| |
| Модуль сдвига Gм, ГПа | |
Коэффициент Пуассона 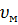
| 0,3 |
Предельное удлинение при растяжении  , % , %
|
Рассмотрим первый случай КМ, когда однонаправленный слой композита состоит из стекловолокон с коэффициентом армирования ψ = 0,6 и полиимидной матрицы.
Модуль упругости при растяжении однонаправленного слоя вдоль волокон определяется по формуле:
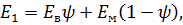 (10)
(10)
где 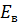 – модуль упругости волокна,
– модуль упругости волокна,
ψ – коэффициент армирования,
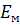 – модуль упругости матрицы.
– модуль упругости матрицы.
Подставив значения упругих свойств компонент, получим модуль упругости при растяжении 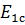 однонаправленного слоя, армированного стекловолокном:
однонаправленного слоя, армированного стекловолокном:
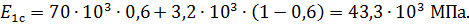 (11)
(11)
Поперечный модуль упругости равен:
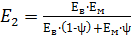 , (12)
, (12)
Подставив данные, получим поперечный модуль упругости 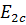 однонаправленного слоя, армированного стекловолокном:
однонаправленного слоя, армированного стекловолокном:
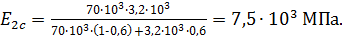 (13)
(13)
Модуль сдвига рассчитывается по формуле:
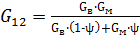 , (14)
, (14)
где 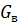 – модуль сдвига волокна,
– модуль сдвига волокна,
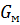 – модуль сдвига матрицы.
– модуль сдвига матрицы.
Подставляя данные в формулу 14, получим модуль сдвига 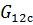 однонаправленного слоя, армированного стекловолокном:
однонаправленного слоя, армированного стекловолокном:
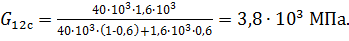 (15)
(15)
Коэффициент Пуассона высчитывается по формуле:
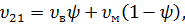 (16)
(16)
где 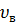 – коэффициент Пуассона волокна,
– коэффициент Пуассона волокна,
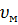 – коэффициент Пуассона матрицы.
– коэффициент Пуассона матрицы.
Подставив данные, получим коэффициент Пуассона 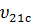 однонаправленного слоя, армированного стекловолокном:
однонаправленного слоя, армированного стекловолокном:
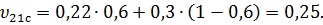 (17)
(17)
Коэффициент υ12 Пуассона определяется из условия ортотропности (наличия трех плоскостей упругой симметрии):
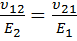 , (18)
, (18)
откуда
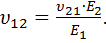 (19)
(19)
Подставив значения, получим коэффициент Пуассона 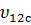 однонаправленного слоя, армированного стекловолокном:
однонаправленного слоя, армированного стекловолокном:
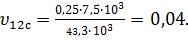 (20)
(20)
Для второго случая, когда однонаправленный слой композита состоит из бороволокон с коэффициентом армирования ψ = 0,6 и полиимидной матрицы, упругие характеристики, подставив в формулы 10, 12, 14, 16 и 19 данные для бороволокна, будут следующие:
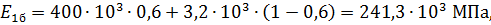 (21)
(21)
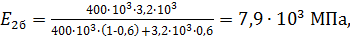 (22)
(22)
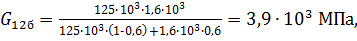 (23)
(23)
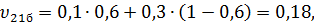 (24)
(24)
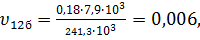 (25)
(25)
где 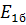 – модуль упругости при растяжении однонаправленного слоя, армированного бороволокном;
– модуль упругости при растяжении однонаправленного слоя, армированного бороволокном;
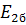 – поперечный модуль упругости однонаправленного слоя, армированного бороволокном;
– поперечный модуль упругости однонаправленного слоя, армированного бороволокном;
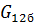 – модуль сдвига однонаправленного слоя, армированного бороволокном;
– модуль сдвига однонаправленного слоя, армированного бороволокном;
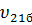 и
и 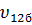 – коэффициенты Пуассона однонаправленного слоя, армированного бороволокном;
– коэффициенты Пуассона однонаправленного слоя, армированного бороволокном;
6 Определение прочности при растяжении и сжатии вдоль волокон
однонаправленного слоя
Определяем прочность при растяжении и сжатии вдоль волокон однонаправленных слоёв. В первом случае однонаправленный слой состоит из стекловолокон диаметром 15 мкм и полиимидной матрицы, а во втором случае – из бороволокон диаметром 50 мкм и полиимидной матрицы. Механические свойства волокон представлены в таблице 4, а матрицы – в таблице 5.
Таблица 4 – Механические свойства стекловолокон и бороволокон
| Механические свойства | Бороволокно | Стекловолокно |
Предел прочности при растяжении вдоль волокон  , МПа , МПа
| ||
| Модуль упругости волокна Ев, МПа | 400 ∙ 103 | 70 ∙ 103 |
Предельное относительное удлинение волокна при растяжении  , % , %
| ||
Предельное относительное удлинение волокна при сжатии  , % , %
| 0,5 | 1,7 |
Таблица 5 – Механические свойства полиимидной матрицы
| Модуль упругости Ем, МПа | 3,2 ∙ 103 |
Предельное относительное удлинение  , % , %
|
Из исходных данных видим, что предельное удлинение матрицы больше предельного удлинения волокна. Следовательно, прочность однонаправленного композита будет определяться прочностью волокон, так как первыми будут разрушаться волокна.
Определяющее уравнение для этого случая, выведенное из условия равновесия сил в направлении укладки волокон и из допущения однородности деформации в направлении действия нагрузки ε1 = εв1 = εм1 имеет вид:
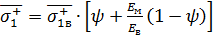 . (26)
. (26)
Подставив исходные данные для стекловолокна и бороволокна, получим:
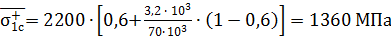 , (27)
, (27)
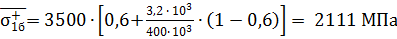 , (28)
, (28)
где 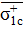 – предел прочности при растяжении однонаправленного слоя, армированного стекловолокном;
– предел прочности при растяжении однонаправленного слоя, армированного стекловолокном;
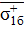 – предел прочности при растяжении однонаправленного слоя, армированного бороволокном.
– предел прочности при растяжении однонаправленного слоя, армированного бороволокном.
Напряжение в матрице в момент разрушения волокна определяется предельной деформацией волокна.
Определение прочности однонаправленного слоя в направлении армирования на сжатие зависит от того, что явилось причиной разрушения: разрушение волокон, разрушение связующего, нарушение прочности сцепления волокна и матрицы либо их сочетание.
Прочность при сжатии определяем по формуле:
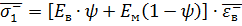 . (29)
. (29)
В первом приближении можно принять, что 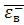 равняется предельной деформации однонаправленного пластика при сжатии. Предполагается также, что армированный пластик деформируется линейно вплоть до разрушения.
равняется предельной деформации однонаправленного пластика при сжатии. Предполагается также, что армированный пластик деформируется линейно вплоть до разрушения.
Подставляя исходные данные, получим:
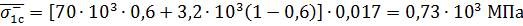 , (30)
, (30)
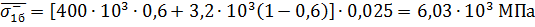 , (31)
, (31)
где 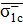 – предел прочности при сжатии однонаправленного слоя, армированного стекловолокном;
– предел прочности при сжатии однонаправленного слоя, армированного стекловолокном;
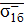 – предел прочности при сжатии однонаправленного слоя, армированного бороволокном.
– предел прочности при сжатии однонаправленного слоя, армированного бороволокном.
Вычисленная прочность однонаправленных слоёв получена в предположении абсолютной адгезии волокон к матрице, их абсолютной прямолинейности, параллельности и равномерного распределения в матрице. Считается также, что поры в однонаправленном композите отсутствуют. Реальная прочность будет отличаться от вычисленной в связи с тем, что удовлетворить всем принятым предпосылкам на практике практически не возможно. Величина расхождения расчетной и реальной прочности будет зависеть от степени их удовлетворения.
Дата добавления: 2016-01-26; просмотров: 4477;
